Câu 82: Cho Tam giác ABC có AB < AC. Trên tia dối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.
a) Hãy so sánh các góc AMB và ANC.
b) Hãy so sánh các độ dài AM và AN.
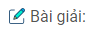
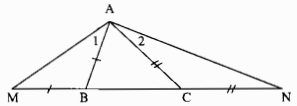
Trong ∆ABC có AB < AC
\( \Rightarrow \) \(\widehat {ABC} = \widehat {ACB}\) (đối diện cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt)
\( \Rightarrow \) ∆ABM cân tại B
\( \Rightarrow \) \(\widehat M = \widehat {{A_1}}\) (tính chất tam giác cân)
Trong ∆ABM ta có có góc ngoài tại đỉnh B
\(\widehat {ABC} = \widehat M + \widehat {{A_1}}\)
Suy ra: \(\widehat M = {1 \over 2}\widehat {ABC}\) (2)
Ta có: AC = CN (gt)
\( \Rightarrow \) ∆CAN cân tại C
\( \Rightarrow \) \(\widehat N = \widehat {{A_2}}\) (tính chất tam giác cân)
Trong ∆CAN ta có \(\widehat {ACB}\) là góc ngoài tại đỉnh C.
\( \Rightarrow \widehat {ACB} = \widehat N + \widehat {{A_2}}\)
Suy ra: \(\widehat N = {1 \over 2}\widehat {ACB}\) (3)
Từ (1), (2) và (3) suy ra: \(\widehat M > \widehat N\)
b) Trong ∆AMN ta có: \(\widehat M > \widehat N\)
Suy ra: AN > AM (đối diện góc lớn hơn là cạnh lớn hơn)
Câu 83: Cho tam giác ABC có AB < AC, đường cao AH. Chứng minh rằng:
Advertisements (Quảng cáo)
HB < HC, \(\widehat {HAB} < \widehat {HAC}\) (xét hai trường hợp: \(\widehat B\) nhọn và \(\widehat B\) tù).
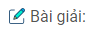
a)
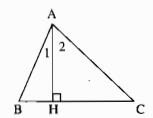
Trường hợp: \(\widehat B < 90^\circ \)
Đường xiên AB < AC nên hình chiếu HB < HC
Trong ∆ABC ta có: AB < AC
\( \Rightarrow \widehat B < \widehat C\) (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow \widehat B + \widehat {HAC} = 90^\circ \) (tính chất tam giác vuông) (1)
Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)
\( \Rightarrow \widehat C + \widehat {HAC} = 90^\circ \) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: \(\widehat B + \widehat {HAB} = \widehat C + \widehat {HAC}\)
Mà \(\widehat B > \widehat C\) nên \(\widehat {HAB} < \widehat {HAC}\)
Advertisements (Quảng cáo)
b)
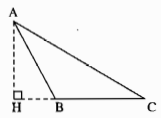
Nếu \(90^\circ < \widehat B < 180^\circ \) điểm B nằm giữa H và C.
\(\widehat {HAC} = \widehat {HAB} + \widehat {BAC}\)
\( \Rightarrow \widehat {HAB} < \widehat {HAC}\)
Câu 84
Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm.
1 = 3 – 2 = 4 – 3 = 5 – 4
Nên trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.
Nếu cạnh nhỏ nhất là 2cm
4 – 3 < 2 < 4 + 3; 5 – 4 < 2 < 5 + 4
Thì 2 cạnh kia là 3cm và 4cm hoặc 4cm và 5cm.
Nếu cạnh nhỏ nhất là 3cm
5 – 4 < + < 5 + 4; 3 = 5 – 2; 3 > 4 – 2
Như vậy hai cạnh kia là 5 và 4.
Không có trường hợp cạnh nhỏ nhất là 4cm.
Vậy ta có thể vẽ được 3 tam giác có ba cạnh là:
2cm; 3cm; 4cm
2cm; 4cm; 5cm
3cm; 4cm; 5cm
Câu 85: Cho bốn điểm A, B, C, D như hình dưới. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.
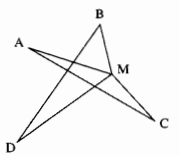
Với M là điểm bất kỳ.
Ta có M không trùng với giao điểm của AC và BD
Trong ∆MBD ta có:
MB + MD > BD (bất đẳng thức tam giác)
Nếu M trùng với giao điểm AC và BD
\( \Rightarrow \) MA + MC = AC
MB + MD = BD
Vậy MA + MC ≥ AC
MB + MD ≥ BD
(dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)
\( \Rightarrow \) MA + MB + MC + MD ≥ AC + BD
Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD

