Câu 70: Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó?
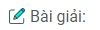
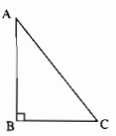
∆ABC vuông tại B => \(AB \bot BC\) nên AB là đường cao từ đỉnh A.
\( \Rightarrow CB \bot AB\) nên CB là đường cao kẻ từ đỉnh C.
B là giao điểm của 2 đường cao AB và CB. Vậy B là trực tâm của ∆ABC.
Câu 71: Cho hình bên.
a) Chứng minh rằng: \(CI \bot AB.\)
b) Cho \(\widehat {ACB} = 40^\circ \). Tính \(\widehat {BI{\rm{D}}},\widehat {DIE}\)
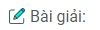
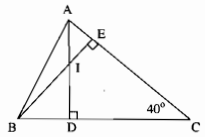
a) Trong ∆ABC ta có hai đường cao AD và BE cắt nhau tại I nên I là trực tâm của ∆ABC
\( \Rightarrow \) CI là đường cao thứ ba
Vậy \(CI \bot AB\)
b) Trong tam giác vuông BEC có
\(\widehat {BEC} = 90^\circ \)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {EBC} + \widehat C = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {EBC} = 90^\circ – \widehat C = 90^\circ – 40^\circ = 50^\circ \) hay \(\widehat {IB{\rm{D}}} = 50^\circ \)
Trong tam giác IDB có \(\widehat {I{\rm{DB}}} = 90^\circ \)
\( \Rightarrow \widehat {IB{\rm{D}}} + \widehat {BI{\rm{D}}} = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {BI{\rm{D}}} = 90^\circ – \widehat {IB{\rm{D}}} = 90^\circ – 50^\circ = 40^\circ \)
\(\widehat {BI{\rm{D}}} + \widehat {DIE} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {DIE} = 180^\circ – \widehat {BI{\rm{D}}} = 180^\circ – 40^\circ = 140^\circ \)
Câu 72: Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC.
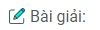
Advertisements (Quảng cáo)
Trong ∆ABC ta có H là trực tâm nên
\(AH \bot BC,BH \bot AC,CH \bot AB\)
Trong ∆AHB ta có:
\(\eqalign{
& AC \bot BH \cr
& BC \bot AH \cr} \)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\eqalign{
& BA \bot CH \cr
& CB \bot BH \cr} \)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\eqalign{
& BA \bot HC \cr
& CA \bot BH \cr} \)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.
Câu 73: Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác cân đó là tam giác cân.
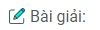
Xét hai tam giác vuông BDC và CEB:
\(\widehat {B{\rm{D}}C} = \widehat {CEB} = 90^\circ \)
BD = CE (gt)
BC cạnh huyền chung
Do đó: ∆BDC = ∆CEB (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \) \(\widehat {DCB} = \widehat {EBC}\)
Hay \(\widehat {ACB} = \widehat {ABC}\)
Vậy ∆ABC cân tại A.

