Câu 9.4: Cho tam giác nhọn ABC cân tại đỉnh A. Hai đường cao xuất phát từ đỉnh B và đỉnh C cắt nhau tại M. Hãy tìm các góc của tam giác ABC, biết \(\widehat {BMC} = 140^\circ \).
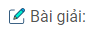
Xét tam giác vuông BKM. Do \(\widehat {BMC} = 140^\circ \) nên \(\widehat {{B_1}} = 140^\circ – 90^\circ = 50^\circ \)
Trong tam giác vuông AHB có
$$\widehat A = 90^\circ – \widehat {{B_1}} = 90^\circ – 50^\circ = 40^\circ $$
Tam giác ABC cân tại A, có Â = 40° nên \(\widehat B = \widehat C = \left( {180^\circ – 40^\circ } \right):2 = 70^\circ \).
Advertisements (Quảng cáo)
Câu 9.5: Chứng minh rằng trong một tam giác, tia phân giác của một góc trong và hai tia phân giác của hai góc ngoài không kề với nó đồng quy tại một điểm, điểm đó cách đều ba đường thẳng chứa ba cạnh của tam giác.
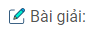
Giả sử hai tia phân giác của các góc ngoài tại đỉnh B và C của tam giác ABC cắt nhau tại O. Ta sẽ chứng minh AO là tia phân giác của góc A.
Advertisements (Quảng cáo)
Kẻ các đường vuông góc OH, OI, OK từ O lần lượt đến các đường thẳng AB, BC, AC.
Vì BO là tia phân giác của góc HBC nên OH = OI (1)
Vì CO là tia phân giác của góc KCB nên OI = OK (2)
Từ (1) và (2) suy ra OI = OH = OK (3)
Từ (3) suy ra AO là tia phân giác của góc BAC và ta có điều phải chứng minh.
Câu 9.6: Cho tam giác ABC, Hai đường phân giác của các cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cắt nhau tại A’, B’, C’. Chứng minh rằng AA’, BB’, CC’ là các đường cao của tam giác A’B’C’. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A’B’C’.
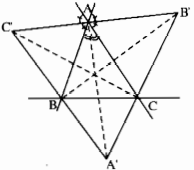
Ta có \({\rm{AA}}’ \bot AB’\) vì chúng là hai tia phân giác của hai góc kề bù. Tương tự \({\rm{AA}}’ \bot AC’\). Vì qua A chỉ có một đường vuông góc với AA’ nên ba điểm B’, A, C’ thẳng hàng và \({\rm{AA}}’ \bot B’C’\), hay A’A là một đường cao của tam giác A’B’C’. Hoàn toàn tương tự ta chứng minh được BB’ và CC’ là hai đường cao của tam giác A’B’C’.
Mặt khác theo cách chứng minh của bài 9.5 ta có AA’, BB’, CC’ là ba tia phân giác của các góc A, B, C của tam giác ABC.Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A’B’C’.

