Bài 1: Trong các mệnh đề sau, mệnh đề nào đúng?
a) Đường thẳng song song với trục Ox có phương trình \(y = m(m \ne 0)\);
b) Đường thẳng có phương trình \(x = {m^2} + 1\) song song với trục Oy;
c) Phương trình \(y = kx + b\) là phương trình của đường thẳng;
d) Mọi đường thẳng đều có phương trình dạng \(y = kx + b\) ;
e) Đường thẳng đi qua hai điểm A(a, 0) và B(0, b) có phương trình \({x \over a} + {y \over b} = 1\)
a) Đúng b) Đúng
c) Đúng d) Sai
e) Sai
Bài 2: Viết phương trình tổng quát của:
a) Đường thẳng Ox;
b) Đường thẳng Oy;
Advertisements (Quảng cáo)
c) Đường thẳng đi qua \(M({x_0};{y_0})\) và song song với Ox;
d) Đường thẳng đi qua \(M({x_0};{y_0})\) và vuông góc với Ox;
e) Đường thẳng OM, với \(M({x_0};{y_0})\) khác điểm O.
a) Đường thẳng Ox đi qua O(0, 0) có véc tơ pháp tuyến \(\overrightarrow n (0;1)\) nên có phương trình tổng quát là:
\(0.(x – 0) + 1.(y – 0) = 0 \Leftrightarrow y = 0\)
b) Đường thẳng Oy đi qua O(0, 0) có véc tơ pháp tuyến \(\overrightarrow n (1;0)\) nên có phương trình tổng quát là:
\(1.(x – 0) + 0.(y – 0) = 0 \Leftrightarrow x = 0\)
Advertisements (Quảng cáo)
c) ) Đường thẳng đi qua \(M({x_0};{y_0})\) và song song với Ox có vectơ pháp tuyến \(\overrightarrow n (0;1)\) nên có phương trình tổng quát là:
\(0.(x – {x_0}) + 1.(y – {y_0}) = 0 \Leftrightarrow y – {y_0} = 0,({y_0} \ne 0)\)
d) Đường thẳng đi qua \(M({x_0};{y_0})\) và vuông góc với Ox có vectơ pháp tuyến \(\overrightarrow n (1;0)\) nên có phương trình tổng quát là:
\(1.(x – {x_0}) + 0.(y – {y_0}) = 0 \Leftrightarrow x – {x_0} = 0,({x_0} \ne 0)\)
e) \(\overrightarrow {OM} ({x_0};{y_0})\) nên đường thẳng OM có véc tơ pháp tuyến là: \(\overrightarrow n ({y_0}; – {x_0})\) .
Phương trình tổng quát của đường thẳng OM là:
\({y_0}(x – 0) – {x_0}(y – 0) = 0 \Leftrightarrow {y_0}x – {x_0}y = 0\
Bài 3: Cho tam giác ABC có phương trình các đường thẳng AB,BC,CA là
\(\eqalign{
& AB:2x – 3y – 1 = 0; \cr
& BC:x + 3y + 7 = 0; \cr
& CA:5x – 2y + 1 = 0. \cr} \)
Viết phương trình tổng quát của đường cao kẻ từ đỉnh B.
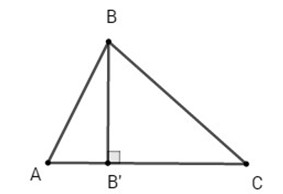
Hai đường thẳng AB,BC cắt nhau tại B nên tọa độ của B là nghiệm của hệ phương trình sau:
\(\left\{ \matrix{
2x – 3y – 1 = 0 \hfill \cr
x + 3y + 7 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = – 2 \hfill \cr
y = – {5 \over 3} \hfill \cr} \right.\)
Vậy \(B\left( { – 2; – {5 \over 3}} \right)\)
Đường thẳng CA có véc tơ pháp tuyến \(\overrightarrow n (5; – 2)\) nên có véc tơ chỉ phương là \(\overrightarrow u (2;5)\)
Đường cao kẻ từ đỉnh B vuông góc với CA nên nhận véc tơ chỉ phương là \(\overrightarrow u (2;5)\) của CA làm véc tơ pháp tuyến.
Phương trình tổng quát của đường cao kẻ từ đỉnh B đi qua \(B\left( { – 2; – {5 \over 3}} \right)\) và có véc tơ pháp tuyến \(\overrightarrow u (2;5)\) là:
\(2.(x + 2) + 5.\left( {y + {5 \over 3}} \right) = 0 \Leftrightarrow 2x + 5y + {{37} \over 3} = 0\)

