Bài Đề toán tổng hợp chương III phần hình học Sách bài tập Toán Hình Học 10. Giải bài 3.54, 3.55, 3.56, 3.57 trang 163 Sách bài tập Toán Hình Học 10. Câu 3.54: Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD có điểm I(6;2) …
Bài 3.54: Trong mặt phẳng tọa độ Oxy cho hình chữ nhật ABCD có điểm I(6;2) là giao điểm của hai đường chéo AC và BD. Điểm M(1;5) thuộc đường thẳng AB và trung điểm E của cạnh CD thuộc đường thẳng \(\Delta 😡 + y – 5 = 0\). \(\Delta 😡 + y – 5 = 0\)

(Xem hình 3.14)
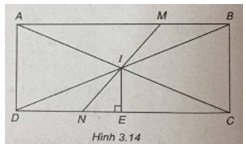
Gọi N là điểm đối xứng với M qua I, suy ra N(11 ; -1) và điểm N thuộc đường thẳng CD.
\(E \in \Delta \Rightarrow E(x;5 – x)\,;\,\overrightarrow {IE} = (x – 6;3 – x)\)
và: \(\overrightarrow {NE} = (x – 11;6 – x)\)
E là trung điểm của CD \( \Rightarrow IE \bot EN.\)
\(\overrightarrow {IE} .\overrightarrow {NE} = 0 \Leftrightarrow \left( {x – 6} \right)\left( {x – 11} \right) + \left( {3 – x} \right)\left( {6 – x} \right) = 0\)
\(\overrightarrow {IE} .\overrightarrow {NE} = 0 \Leftrightarrow \left( {x – 6} \right)\left( {x – 11} \right) + \left( {3 – x} \right)\left( {6 – x} \right) = 0\)
\( \Leftrightarrow x = 6\) hoặc x = 7
Với \(x = 6 \Rightarrow \overrightarrow {IE} = (0;3),\)
Phương trình \(AB:y – 5 = 0.\)
Với \(x = 7 \Rightarrow IE = \left( {1; – 4} \right),\)
Phương trình \(AB:x – 4y + 19 = 0.\)
Bài 3.55: Trong mặt phẳng tọa độ Oxy cho đường tròn (C) : \({(x – 2)^2} + {y^2} = {4 \over 5}\) và đường thẳng \({\Delta _1}:x – y = 0\), \({\Delta _2}:x – 7y = 0\). Xác định tọa độ tâm K vàn bán kính của đường tròn (C1) ; biết đường tròng (C1) tiếp xúc với các đường thẳng \({\Delta _1}\), \({\Delta _2}\) và tâm K không thuộc đường tròn (C).
Advertisements (Quảng cáo)

(Xem hình 3.15)
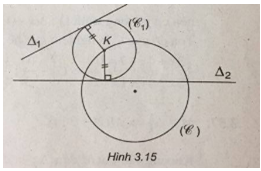
Gọi \(K\left( {a;b} \right)\,;\,k \in (C) \Leftrightarrow {\left( {a – 2} \right)^2} + {b^2} = {5 \over 4}\,\,\,\,\,(1)\)
\(({C_1})\) tiếp xúc với \({\Delta _1},{\Delta _2} \Leftrightarrow {{\left| {a – b} \right|} \over {\sqrt 2 }} = {{\left| {a – 7b} \right|} \over {5\sqrt 2 }}\,\,(2).\)
Từ (1) và (2) cho ta :
\(\left\{ \matrix{
5{\left( {a – 2} \right)^2} + 5{b^2} = 4 \hfill \cr
5\left| {a – b} \right| = \left| {a – 7b} \right| \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{
5{\left( {a – 2} \right)^2} + 5{b^2} = 4 \hfill \cr
5\left( {a – b} \right) = a – 7b \hfill \cr} \right.\,\,\,\,(I)\,\,\,\)
và \(\left\{ \matrix{
5{\left( {a – 2} \right)^2} + 5{b^2} = 4 \hfill \cr
5(a – b) = 7b – a \hfill \cr} \right.\,\,\,\,\,\,(II)\)
\((I) \Leftrightarrow \left\{ \matrix{
25{a^2} – 20a + 16 = 0 \hfill \cr
b = – 2a \hfill \cr} \right.\)
Advertisements (Quảng cáo)
(vô nghiệm)
\((II) \Leftrightarrow \left\{ \matrix{
a = 2b \hfill \cr
25{b^2} – 40b + 16 = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left( {a;b} \right) = \left( {{8 \over 5};{4 \over 5}} \right).\)
Bán kính (C1): \(R = {{\left| {a – b} \right|} \over {\sqrt 2 }} = {{2\sqrt 2 } \over 5}.\)
Vậy \(K\left( {{8 \over 5};{4 \over 5}} \right)\) và \(R = {{2\sqrt 2 } \over 5}.\)
Bài 3.56: Trong mặt phẳng tọa độ Oxy, hãy xác định tọa độ đỉnh C của tam giác ABC biết rằng hình chiếu vuông góc của C trên đường thẳng AB là điểm H(-1;-1), đường phân giác trong của góc A có phương trình x – y + 2 = 0 và đường cao kẻ từ B có phương trình 4x + 3y – 1 = 0

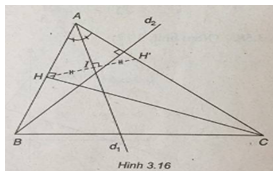
Ta gọi \({d_1}:x – y + 2 = 0\) và \({d_2}:4x + 3y – 1 = 0\).
Gọi H'(a;b) là điểm đối xứng của H qua \({d_1}\)
Khi đó H’ thuộc đường thẳng AC (h.3.16).
\(\overrightarrow u = (1;1)\) là vectơ chỉ phương của \({d_1}\), \(\overrightarrow {HH’} = \left( {a + 1;b + 1} \right)\) vuông góc với \(\overrightarrow u \) và trung điểm \(I\left( {{{a – 1} \over 2};{{b – 1} \over 2}} \right)\) của \(\overrightarrow {HH’} \) thuộc \({d_1}\). Do đó tọa độ của H’ là nghiệm của hệ phương trình:
\(\left\{ \matrix{
1.\left( {a + 1} \right) + 1\left( {b + 1} \right) = 0 \hfill \cr
{{a – 1} \over 2} – {{b – 1} \over 2} = 0 \hfill \cr} \right. \Rightarrow H'( – 3;1).\)
Đường thẳng AC đi qua H’ vuông góc với \({d_2}\) nên có viectơ pháp tuyến là \(\overrightarrow v = \left( {3; – 4} \right)\), suy ra AC có phương trình là :
\(\eqalign{
& 3\left( {x + 3} \right) – 4\left( {y – 1} \right) = 0 \cr
& \Leftrightarrow 3x – 4y + 13 = 0. \cr} \)
Tọa độ của A là nghiệm của hệ phương trình \(\left\{ \matrix{
3x – 4y + 13 = 0 \hfill \cr
x – y + 2 = 0 \hfill \cr} \right.\)
\( \Rightarrow A(5;7).\)
Đường thẳng CH đi qua H (-1 ; -1) với vectơ pháp tuyến là \({1 \over 2}\overrightarrow {HA} = \left( {3;4} \right)\) nên có phương trình là:
\(3\left( {x + 1} \right) + 4\left( {y + 1} \right) = 0 \Leftrightarrow 3x + 4y + 7 = 0.\)
Tọa độ của C là nghiệm của phương trình
\(\left\{ \matrix{
3x + 4y + 7 = 0 \hfill \cr
3x – 4y + 13 = 0 \hfill \cr} \right. \Rightarrow C\left( { – {{10} \over 3};{3 \over 4}} \right).\)
Bài 3.57: Trong mặt phẳng tọa độ Oxy, cho các đường thẳng \({\Delta _1}:x – 2y – 3 = 0\) và \({\Delta _2}:x + y + 1 = 0\). Tìm tọa độ điểm M thuộc đường thẳng \({\Delta _1}\) sao cho khoảng cách từ M đến đường thẳng \({\Delta _2}\) bằng \({1 \over {\sqrt 2 }}\).

Khoảng cách từ M đến \({\Delta _2}\) là \(d(M,{\Delta _2}) = {{\left| {2t + 3 + t + 1} \right|} \over {\sqrt 2 }}\)
\(d(M,{\Delta _2}) = {1 \over {\sqrt 2 }} \Leftrightarrow \left[ \matrix{
t = – 1 \hfill \cr
t = – {5 \over 3} \hfill \cr} \right.\)
Vậy M(1;-1) hoặc \(M\left( { – {1 \over 3}; – {5 \over 3}} \right).\)

