Bài 1.61: Cho các điểm A'(-4;1), B'(2;4) và C'(2; – 2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC.
a) Tính tọa độ các đỉnh của tam giác ABC;
b) Chứng minh rằng các trọng tâm của các tam giác ABC và A’B’C’ trùng nhau.

(Xem hình 1.72)
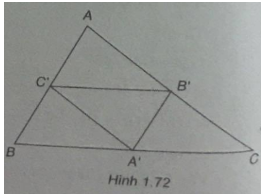
a)
\(\overrightarrow {C’A} = \overrightarrow {A’B’} = > \left\{ \matrix{
{x_A} – 2 = 6 \hfill \cr
{y_A} + 2 = 3 \hfill \cr} \right. = > \left\{ \matrix{
{x_A} = 8 \hfill \cr
{y_A} = 1 \hfill \cr} \right.\)
\(\overrightarrow {BA’} = \overrightarrow {C’B’} = > \left\{ \matrix{
– 4 – {x_B} = 0 \hfill \cr
1 – {y_B} = 6 \hfill \cr} \right. = > \left\{ \matrix{
{x_B} = – 4 \hfill \cr
{y_B} = – 5 \hfill \cr} \right.\)
\(\overrightarrow {A’C} = \overrightarrow {C’B’} = > \left\{ \matrix{
{x_C} + 4 = 0 \hfill \cr
{y_C} – 1 = 6 \hfill \cr} \right. = > \left\{ \matrix{
{x_C} = – 4 \hfill \cr
{y_C} = 7 \hfill \cr} \right.\)
b) Tính tọa độ trọng tâm G, G’ của tam giác ABC và A’B’C’ ta được G(0;1) và G'(0;1).
Vậy G=G’
Bài 1.62: Cho \(\overrightarrow a = (2; – 2)\) và \(\overrightarrow b = (1;4)\)
a) Tính tọa độ của vec tơ \(\overrightarrow a + \overrightarrow b ;\overrightarrow a – \overrightarrow b \) và \(2\overrightarrow a + 3\overrightarrow b \)
Advertisements (Quảng cáo)
b) Hãy phân tích vec tơ \(\overrightarrow c = (5;0)\) theo hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \)

a) \(\overrightarrow a + \overrightarrow b = (3;2)\)
\(\overrightarrow a – \overrightarrow b = (1; – 6)\)
\(2\overrightarrow a + 3\overrightarrow b = (7;8)\)
b) Giả sử \(c = h\overrightarrow a + k\overrightarrow b \). Khi đó:
\(\left\{ \matrix{
2h + k = 5 \hfill \cr
– 2h + 4k = 0 \hfill \cr} \right. = > \left\{ \matrix{
h = 2 \hfill \cr
k = 1 \hfill \cr} \right.\)
Vậy \(\overrightarrow c = 2\overrightarrow a + \overrightarrow b \)
Advertisements (Quảng cáo)
Bài 1.63: Cho $$\overrightarrow a = (2;1),\overrightarrow b = (3; – 4),\overrightarrow c = ( – 7;2)$$
a) Tìm tọa độ của vec tơ \(\overrightarrow u = 3\overrightarrow a + 2\overrightarrow b – 4\overrightarrow c \)
b) Tìm tọa độ vec tơ \(\overrightarrow x \) sao cho: \(\overrightarrow x + \overrightarrow a = \overrightarrow b – \overrightarrow c \)
c) Tìm các số k và h sao cho: \(\overrightarrow c = k\overrightarrow a + h\overrightarrow b \)

a) \(\overrightarrow u = (3.2 + 2.3 – 4.( – 7);3.1 + 2.( – 4) – 4.2)\)
\(\overrightarrow u = (40; – 13)\)
b) \(\overrightarrow u = \overrightarrow b – \overrightarrow c – \overrightarrow a = (8; – 7)\)
c) \(k\overrightarrow a + h\overrightarrow b = (2k + 3h;k – 4h)\)
\(\overrightarrow c = k\overrightarrow a + h\overrightarrow b \Leftrightarrow \left\{ \matrix{
2k + 3h = – 7 \hfill \cr
k – 4h = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
k = – 2 \hfill \cr
h = – 1 \hfill \cr} \right.\)
Bài 1.64: Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng:
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = {2 \over 3}\overrightarrow {MO} \)

(Xem hình 1.73)
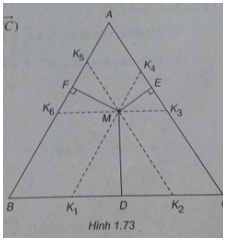
Qua M kẻ các đường thẳng sau: \({K_1}{K_4}\)//AB, \({K_2}{K_5}\)//AC, \({K_3}{K_6}\)//BC
\({K_1},{K_2} \in BC;{K_3},{K_4} \in AC;{K_5},{K_6} \in AB\). Ta có:
\(\eqalign{
& \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} \cr
& = {1 \over 2}(\overrightarrow {M{K_1}} + \overrightarrow {M{K_2}} + \overrightarrow {M{K_3}} + \overrightarrow {M{K_4}} + \overrightarrow {M{K_5}} + \overrightarrow {M{K_6}} ) \cr} \)
\( = {1 \over 2}(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} )\)
(Vì \(M{K_5}A{K_4},M{K_3}C{K_2},M{K_1}B{K_6}\) là các hình bình hành). Vậy
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = {1 \over 2}.3\overrightarrow {MO} = {3 \over 2}\overrightarrow {MO} \)

