Bài 1.52: Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = \overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} \)

(h.1.65)
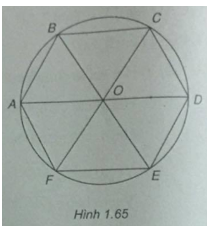
Gọi O là tâm lục giác đều. Khi đó O là trọng tâm của các tam giác đều ACE và BDF.
Do đó, với mọi điểm M ta có:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = 3\overrightarrow {MO} \)
Advertisements (Quảng cáo)
\(\overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} = 3\overrightarrow {MO} \)
Vậy ta có đẳng thức cần chứng minh.
Bài 1.53: Cho tam giác ABC. Tìm điểm M thỏa mãn điều kiện: \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)

(h.1.66)
Advertisements (Quảng cáo)
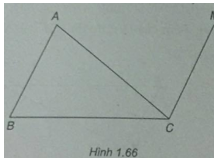
\(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM} $\)
M là đỉnh của hình bình hành ABCM.
Bài 1.54
Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC. BE cắt trung tuyến AM tại N. Tính \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} \)

(h.1.67)
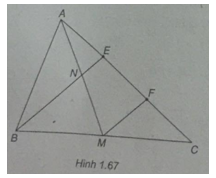
Ta có \(\overrightarrow {AE} = \overrightarrow {FC} \)
Vì MF // BE nên N là trung điểm của AM, suy ra \(\overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow 0 \)
Do đó \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow {AF} + \overrightarrow {FC} = \overrightarrow {AC}\)

