Bài 1.55: Cho hai điểm A và B. Điểm M thỏa mãn điều kiện \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} – \overrightarrow {MB} } \right|\). Chứng minh rằng: \(OM = {1 \over 2}AB\), trong đó O là trung điểm của AB.

(h.1.68)
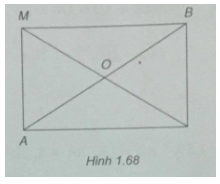
\(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MO} = > \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2MO\)
\(\overrightarrow {MA} – \overrightarrow {MB} = \overrightarrow {BA} = > \left| {\overrightarrow {MA} – \overrightarrow {MB} } \right| = AB\)
Vậy 2MO = AB hay \(OM = {1 \over 2}AB.\)
Chú ý: Tập hợp các điểm M có tính chất \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} – \overrightarrow {MB} } \right|\) là đường tròn đường kính AB.
Bài 1.56: Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vec tơ \(\overrightarrow v = \overrightarrow {MA} + \overrightarrow {MB} – 2\overrightarrow {MC} \) không phụ thuộc vào vị trí của điểm M. Hãy xác định điểm D sao cho \(\overrightarrow {CD} = \overrightarrow v \).

\(\overrightarrow v = \overrightarrow {MA} + \overrightarrow {MB} – 2\overrightarrow {MC}\)
Advertisements (Quảng cáo)
\( = 2\overrightarrow {ME} – 2\overrightarrow {MC} \) (E là trung điểm cạnh AB)
\( = 2(\overrightarrow {ME} – \overrightarrow {MC} ) = 2\overrightarrow {EC} \)
Vậy \(\overrightarrow v \) không phụ thuộc vị trí của điểm M.
\(\overrightarrow {CD} = \overrightarrow v = 2\overrightarrow {CE} \) thì E là trung điểm của CD. Vậy ta xác định được điểm D.
Bài 1.57: Cho tam giác ABC. Gọi M, N , P là những điểm được xác định như sau:
\(\overrightarrow {MB} = 3\overrightarrow {MC} ,\overrightarrow {NC} = 3\overrightarrow {NA} ,\overrightarrow {PA} = 3\overrightarrow {PB} \)
a) Chứng minh \(2\overrightarrow {OM} = 3\overrightarrow {OC} – \overrightarrow {OB} \) với mọi điểm O.
Advertisements (Quảng cáo)
b) Chứng minh hai tam giác ABC và MNP có cùng trọng tâm.

(Xem h.1.69)
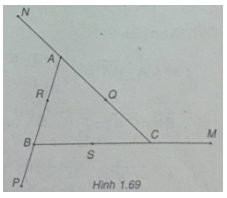
a) $\(3\overrightarrow {OC} – \overrightarrow {OB} = 3(\overrightarrow {OM} + \overrightarrow {MC} ) – (\overrightarrow {OM} + \overrightarrow {MB} )\)
\(= 3(\overrightarrow {OM} – \overrightarrow {OM} ) + (3\overrightarrow {MC} – \overrightarrow {MB} ) = 2\overrightarrow {OM} \)
b) Gọi S, Q và R lần lượt là trung điểm của BC, CA và AB.
\(\overrightarrow {MB} = 3\overrightarrow {MC} = > \overrightarrow {CM} = \overrightarrow {SC} \)
\(\overrightarrow {NC} = 3\overrightarrow {NA} = > \overrightarrow {AN} = \overrightarrow {CQ} \)
\(\overrightarrow {PA} = 3\overrightarrow {PB} = > \overrightarrow {BP} = \overrightarrow {RB} = \overrightarrow {QS} \)
Gọi G là trọng tâm của tam giác ABC thì \(\overrightarrow {GA} + \overrightarrow {BG} + \overrightarrow {GC} = \overrightarrow 0\)
Ta có:
\(\eqalign{
& \overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GP} \cr
& = \overrightarrow {GC} + \overrightarrow {CM} + \overrightarrow {GA} + \overrightarrow {AN} + \overrightarrow {GB} + \overrightarrow {BP} \cr} \)
\(\overrightarrow { = (GA} + \overrightarrow {GC} + \overrightarrow {GC} ) + (\overrightarrow {SC} + \overrightarrow {CQ} + \overrightarrow {QS} )\)
\( = \overrightarrow 0 + \overrightarrow 0 \)
Vậy G là trọng tâm của tam giác MNP.

