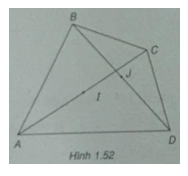
Bài 1.32: Cho tứ giác ABCD. Gọi I và J lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh \(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {IJ} \)

(h.1.52)
\(\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {BJ}\)
\(\overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CD} + \overrightarrow {DJ} \)
Cộng từng vế hai đẳng thức trên ta được
\(\eqalign{
& 2\overrightarrow {IJ} = (\overrightarrow {IA} + \overrightarrow {IC} ) + \overrightarrow {AB} + \overrightarrow {CD} + (\overrightarrow {BJ} + \overrightarrow {DJ} ) \cr
& = \overrightarrow {AB} + \overrightarrow {CD} \cr} \)
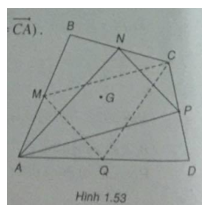
Bài 1.33: Cho tứ giác ABCD. Các điểm M, N , P và Q lần lượt là trung điểm của AB, BC, CD và DA. Chứng minh rằng hai tam giác ANP và CMQ có cùng trọng tâm.

(h.1.53)
Gọi G là trọng tâm của tam giác ANP.
Khi đó $\(\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP} = \overrightarrow 0 \)
Ta có:
\(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow {GA} + \overrightarrow {AC} + \overrightarrow {GN} + \overrightarrow {NM} + \overrightarrow {GP} + \overrightarrow {PQ} \)
\( = (\overrightarrow {GA} + \overrightarrow {GN} + \overrightarrow {GP} ) + \overrightarrow {AC} + (\overrightarrow {NM} + \overrightarrow {PQ} )\)
\(\overrightarrow { = AC} + \overrightarrow {CA} = \overrightarrow 0 \)
(Vì \(\overrightarrow {NM} = {1 \over 2}\overrightarrow {CA} ,\overrightarrow {PQ} = {1 \over 2}\overrightarrow {CA}\) nên \(\overrightarrow {NM} + \overrightarrow {PQ} = \overrightarrow {CA} \))
Advertisements (Quảng cáo)
Vậy \(\overrightarrow {GC} + \overrightarrow {GM} + \overrightarrow {GQ} = \overrightarrow 0 \)
Suy ra G là trọng tâm của tam giác CMQ.
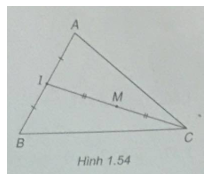
Bài 1.34: Cho tam giác ABC.
a)Tìm điểm K sao cho \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {CB} \)
b)Tìm điểm M sao cho \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)

(Xem h.1.54)
a) \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {CB} \)
\(\Leftrightarrow \overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {KB} – \overrightarrow {KC} \)
\( \Leftrightarrow \overrightarrow {KA} + \overrightarrow {KB} + \overrightarrow {KC} = \overrightarrow 0 \)
K là trọng tâm của tam giác ABC.
Advertisements (Quảng cáo)
b) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {MI} + 2\overrightarrow M C = \overrightarrow 0 \) (I là trung điểm của AB)
Hay \(\overrightarrow {MI} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \) M là trung điểm của IC.
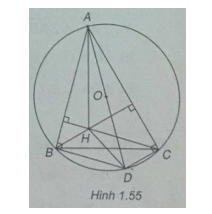
Bài 1.35: Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.
a) Chứng minh tứ giác HCDB là hình bình hành.
b) Chứng minh: \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} \);
\(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \);
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \).
c) Gọi G là trọng tâm tam giác ABC.
Chứng minh \(\overrightarrow {OH} = 3\overrightarrow {OG} \)
Từ đó có kết luận gì về ba điểm O, H, G?

(Xem h.1.55)
a) Vì AD là đường kính của đường tròn tâm O nên \(BD \bot AB,DC \bot AC\)
Ta có \(CH \bot AB,BH \bot AC\) nên suy ra CH // BD và BH // DC.
Vậy tứ giác HCDB là hình bình hành.
b) Vì O là trung điểm của AD nên \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} (1)\)
Vì tứ giác HCDB là hình bình hành nên ta có \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \).
Vậy từ (1) suy ra:
\(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} (2)\)
Theo quy tắc ba điểm, từ (2) suy ra
\(\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {HO} + \overrightarrow {OB} + \overrightarrow {HO} + \overrightarrow {OC} = 2\overrightarrow {HO} \)
Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} (3)\)
c) G là trọng tâm của tam giác ABC.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \)
Từ (3) suy ra \(\overrightarrow {OH} = 3\overrightarrow {OG} \)
Vậy ba điểm O, H, G thẳng hàng.
Trong một tam giác trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O thẳng hàng.

