Câu 42: Trong những hình thoi có chu vi bằng nhau, hãy tìm hình thoi có diện tích lớn nhất.
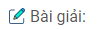
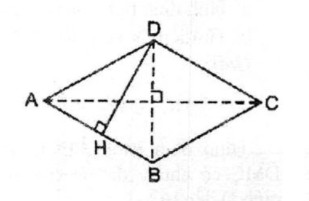
Xét hình thoi ABCD. Kẻ DH ⊥ AB
Ta có: SABCD = AB . DH
∆ AHD vuông tại H ⇒ AH ≤ AD
Suy ra: SABCD ≤ AB . AD, mà AB = AD (gt)
\( \Rightarrow {S_{ABCD}} \le A{B^2}\)
Vậy SABCD có giá trị lớn nhất khi bằng AB2
Suy ra: ABCD là hình vuông
Advertisements (Quảng cáo)
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.
Câu 43: Tính diện tích hình thoi, biết cạnh của nó dài 6,2cm và một trong các góc của nó có số đo bằng 30°
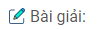
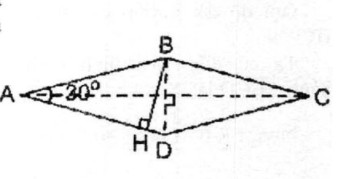
Giả sử hình thoi ABCD có AB = 6,2cm; \(\widehat A = 30^\circ \)
Từ B kẻ BH ⊥ AD (H ∈ AD)
Advertisements (Quảng cáo)
Tam giác vuông AHB là một nửa tam giác đều cạnh AB
\(\eqalign{ & \Rightarrow BH = {1 \over 2}AB = 3,1(cm) \cr & {S_{ABCD}} = BH.AD = 3,1.6,2 = 19,22(c{m^2}) \cr} \)
Câu 44: Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi đó.
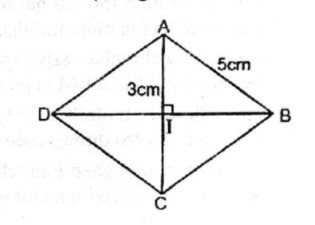
Trong tam giác vuông IAB, ta có:
\(A{B^2} = A{I^2} + I{B^2}\) (định lý Pi-ta-go)
\(\eqalign{ & \Rightarrow I{B^2} = A{B^2} – A{I^2} = 25 – 9 = 16 \cr & \Rightarrow IB = 4(cm) \cr & AC = 2AI = 2.3 = 6(cm) \cr & BD = 2IB = 2.4 = 8(cm) \cr & {S_{ABCD}} = {1 \over 2}AC.BD = {1 \over 2}.6.8 = 24(c{m^2}) \cr} \)
Câu 45: a. Hãy vẽ một tứ giác có hai đường chéo vuông góc với nhau, biết độ dài hai đường chéo đó là a và a. Hỏi có thể vẽ được bao nhiêu hình như vậy ?
b. Có thể vẽ được mấy hình thoi, biết độ dài hai đường chéo là a và \({1 \over 2}\)a ?
c. Hãy tính diện tích các hình vừa vẽ.
a. Vẽ vô số hình tứ giác thỏa mãn yêu cầu.
b. Vẽ được duy nhất một hình thoi có hai đường chéo là a và \({1 \over 2}\)a.
c. Diện tích các hình vẽ đó là : S = \({1 \over 2}\)a. \({1 \over 2}\)a = \({1 \over 4}{a^2}\) (đvdt)

