Câu 77: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
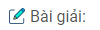
Nối đường chéo AC.
Trong ∆ ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của ∆ ABC
⇒ EF // AC và EF \( = {1 \over 2}\)AC (tính chất đường trung bình tam giác) (1)
Trong ∆ ADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG \( = {1 \over 2}\)AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
Câu 78: Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD , AB. Đường chéo BD cắt AI, CK theo thứ tự ở E, F. Chứng minh rằng DE = EF = FB.
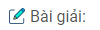
Advertisements (Quảng cáo)
Ta có: AB = CD ( tính chất hình bình hành)
AK \( = {1 \over 2}\)AB (gt)
CI \( = {1 \over 2}\)CD (gt)
Suy ra: AK = CI (1)
Mặt khác: AB // CD (gt)
⇒ AK // CI (2)
Từ (1) và (2) suy ra tứ giác AKCI là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ AI // CK
Trong ∆ ABE ta có:
K là trung điểm của AB (gt)
AI // CK hay KF // AE nên BF // EF ( tính chất đường trung bình tam giác)
Advertisements (Quảng cáo)
Trong ∆ DCF ta có:
I là trung điểm của DC (gt)
AI // CK hay IE // CF nên DE = EF (tính chất đường trung bình tam giác)
Suy ra: DE = EF = FB
Câu 79: Tính các góc của hình bình hành ABCD, biết:
a. \(\widehat A = {110^0}\)
b. \(\widehat A – \widehat B = {20^0}\)
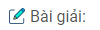
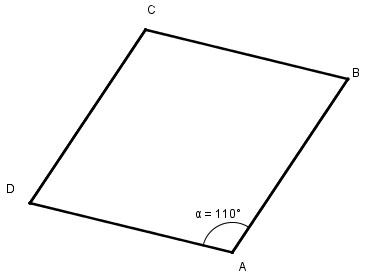
a. Tứ giác ABCD là hình bình hành.
\( \Rightarrow \widehat C = \widehat A = {110^0}\) (tính chất hình bình hành)
\(\widehat A + \widehat B = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat B = {180^0} – \widehat A = {180^0} – {110^0} = {70^0}\)
\(\widehat D = \widehat B = {70^0}\) (tính chất hình bình hành)
b. Tứ giác ABCD là hình bình hành
\( \Rightarrow \widehat A = \widehat B = {180^0}\) (2 góc trong cùng phía bù nhau)
\(\widehat A – \widehat B = {20^0}\) (gt)
Suy ra: \(2\widehat A = {200^0} \Rightarrow \widehat A = {100^0}\)
\(\widehat C = \widehat A = {100^0}\) ( tính chất hình bình hành)
\(\widehat B = \widehat A – {20^0} = {100^0} – {20^0} = {80^0}\)
\(\widehat D = \widehat B = {80^0}\) (tính chất hình bình hành)
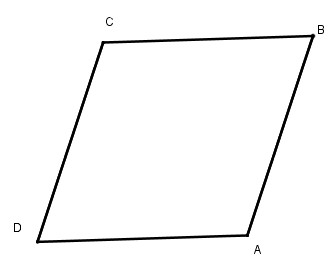
Câu 80: Trong các tứ giác trên hình 9, tứ giác nào là hình bình hành ?
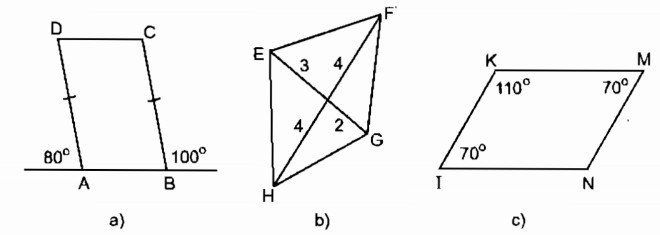
Tứ giác ABCD là hình bình hành vì AB // BC và AD = BC
Tứ giác IKMN là hình bình hành vì có
\(\widehat I = \widehat M = {70^0},\widehat K = \widehat N = {110^0}\).

