Câu 40: Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh rằng MI = IK = KN.
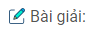
Trong tam giác ABC ta có:
E là trung điểm của cạnh AB
D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
\( \Rightarrow ED//BC\) và \(ED = {1 \over 2}BC\) (tính chất đường trung bình của tam giác)
Trong hình thang BCDE, ta có: BC // DE
M là trung điểm cạnh bên BE
N là trung điểm cạnh bên CD
Nên MN là đường trung bình hình thang BCDE ⇒ MN // DE
\(MN = {{DE + BC} \over 2} = {{{{BC} \over 2} + BC} \over 2} = {{3BC} \over 4}\) (tính chất đường trung bình hình thang)
Trong tam giác BED ta có:
M là trung điểm của BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
\( \Rightarrow MI = {1 \over 2}DE = {1 \over 4}BC\) (tính chất đường trung bình tam giác)
Trong tam giác CED ta có:
N là trung điểm của CD
NK // DE
Suy ra: NK là đường trung bình của ∆ BED
\( \Rightarrow NK = {1 \over 2}DE = {1 \over 4}BC\) (tính chất đường trung bình tam giác)
\(\eqalign{
& IK = MN – \left( {MI + NK} \right) \cr
& = {3 \over 4}BC – \left( {{1 \over 4}BC + {1 \over 4}BC} \right) = {1 \over 4}BC \cr
& \Rightarrow MI = IK = KN = {1 \over 4}BC \cr} \)
Câu 41: Chứng minh rằng đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của hai đường chéo và đi qua trung điểm của cạnh bên thứ hai.
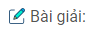
Advertisements (Quảng cáo)
Xét hình thang ABCD có: AB // CD.
E là trung điểm của AD, đường thẳng đi qua E song song với AB cắt BC tại F, AC tại K, BD tại I.
Vì E là trung điểm của AD
EF // AB
Suy ra: BF = FC (tính chất đường trung bình hình thang)
Trong tam giác ADC ta có:
E là trung điểm của AD
EK // DC
Suy ra: AK = KC (tính chất đường trung bình tam giác)
Trong tam giác ABD ta có:
E là trung điểm cạnh AD
EI // AB
Suy ra: BI = ID (tính chất đường trung bình của tam giác)
Vậy đường thẳng đi qua trung điểm E của cạnh bên AD của hình thang ABCD thì đi qua trung điểm cạnh bên BC và trung điểm hai đường chéo AC, BD.
Câu 42: Chứng minh rằng trong hình thang mà hai đáy không bằng nhau, đoạn thẳng nối trung điểm của hai đường chéo bằng nửa hiệu hai đáy.
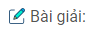
Giả sử hình thang ABCD có AB // CD, AB < CD.
I, K lần lượt là trung điểm hai đường chéo BD, AC
Advertisements (Quảng cáo)
Gọi F là trung điểm của BC
Trong tam giác ACB ta có:
K là trung điểm của cạnh AC
F là trung điểm của cạnh BC
Nên KF là đường trung bình của ∆ BDC
⇒ KF // AB và \(KF = {1 \over 2}AB\) (tính chất đường trung bình của tam giác)
Trong tam giác BDC ta có:
I là trung điểm của cạnh BD
F là trung điểm của cạnh BC
Nên IF là đường trung bình của ∆ BDC
⇒ IF // CD và \(IF = {1 \over 2}CD\) (tính chất đường trung bình của tam giác)
FK // AB mà AB // CD nên FK // CD
FI // CD (chứng minh trên)
Suy ra hai đường thẳng FI và FA trùng nhau.
⇒ I, K, F thẳng hàng, AB < CD ⇒ FK < FI nên K nằm giữa I và F
IF = IK + KF
\(\eqalign{
& \Rightarrow IK = IF – KF \cr
& = {1 \over 2}CD – {1 \over 2}AB = {{CD – AB} \over 2} \cr} \)
Câu 43: Hình thang ABCD có AB // CD, AB = a, BC = b, CD = c, DA = d. Các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N.
a) Chứng ninh rằng MN // CD.
b) Tính độ dài MN theo a, b, c, d (a, b, c, d có cùng đơn vị đo)
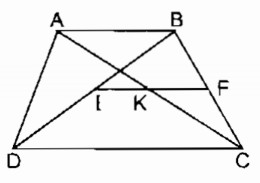
a) Gọi M’ và N’ là giao điểm của tia AM và BN với CD. Ta có:
\(\widehat {M’} = {\widehat A_2}\) (so le trong)
\({\widehat A_1} = {\widehat A_2}\) (gt)
Suy ra: \(\widehat {M’} = {\widehat A_1}\)
Nên ∆ ADM’ cân tại D
DM là phân giác của \(\widehat {ADM’}\)
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM’
\(\widehat {N’} = {\widehat B_2}\) (so le trong)
\({\widehat B_1} = {\widehat B_2}\) (gt)
Suy ra: \(\widehat {N’} = {\widehat B_1}\) nên ∆ BCN’ cân tại C
CN là phân giác của \(\widehat {BCN’}\)
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN’
Suy ra: MN là đường trung bình của hình thang ABN’M’
⇒ MN // M’N’ (tính chất đường trung bình hình thang)
Hay MN // CD
b) \(MN = {{AB + M’N’} \over 2}\) (tính chất đường trung bình của hình thang)
\( \Rightarrow MN = {{AB + M’D + CD + CN’} \over 2}\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Mà M’D = AD, CN’ = BC. Thay vào (1):
\(MN = {{AB + AD + CD + BC} \over 2} = {{a + d + c + b} \over 2}\)

