Câu 7: Cho tứ giác ABCD. Chứng minh rằng tổng hai góc ngoài tại các đỉnh A và C bằng tổng hai góc trong tạo các đỉnh B và D
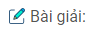
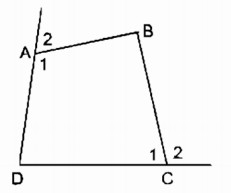
Gọi \(\widehat {{A_1},}\widehat {{C_1}}\) là góc trong của tứ giác tại đỉnh A và C. \({\widehat A_2},{\widehat C_2}\) là góc ngoài tại đỉnh A và C.
Ta có: \({\widehat A_1} + {\widehat A_2} = {180^0}\) (2 góc kề bù)
\(\Rightarrow {\widehat A_2} = {180^0} – {\widehat A_1}\)
\({\widehat C_1} + {\widehat C_2} = {180^0}\) (2 góc kề bù)
\( \Rightarrow {\widehat C_2} = {180^0} – {\widehat C_1}\)
Suy ra:
\(\eqalign{
& {\widehat A_2} + {\widehat C_2} = {180^0} – {\widehat A_1} + {180^0} – {\widehat C_1} \cr
& = {360^0} – \left( {{{\widehat A}_1} + {{\widehat C}_1}} \right) \cr}\) (1)
Trong tứ giác ABCD ta có:
\({\widehat A_1} + \widehat B + {\widehat C_1} + \widehat D = {360^0}\) (tổng các góc của tứ giác)
\(\Rightarrow \widehat B + \widehat D = {360^0} – \left( {{{\widehat A}_1} + {{\widehat C}_1}} \right)\) (2)
Từ (1) và (2) suy ra: \({\widehat A_2} + {\widehat C_2} = \widehat B + \widehat D\)
Câu 8: Tứ giác ABCD có \(\widehat A = {110^0},\widehat B = {100^0}\). Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính \(\widehat {CED},\widehat {CFD}\)
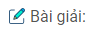
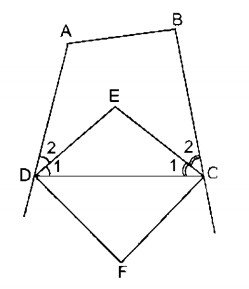
– Trong tứ giác ABCD, ta có:
\(\eqalign{
& \widehat A + \widehat B + \widehat C + \widehat D = {360^0} \cr
& \Rightarrow \widehat C + \widehat D = {360^0} – \left( {\widehat A + \widehat B} \right) \cr
& = {360^0} – \left( {{{110}^0} + {{100}^0}} \right) = {150^0} \cr
& {\widehat D_1} + {\widehat C_1} = {{\widehat C + \widehat D} \over 2} = {{{{150}^0}} \over 2} = {75^0} \cr} \)
– Trong ∆CED, ta có:
Advertisements (Quảng cáo)
\(\widehat {CED} = {180^0} – \left( {{{\widehat C}_1} + {{\widehat D}_1}} \right) = {180^0} – {75^0} = {105^0}\)
DE ⊥ DF (tính chất tia phân giác của hai góc kề bù)
\(\Rightarrow \widehat {EDF} = {90^0}\)
CE ⊥ CF (tính chất tia phân giác của hai góc kề bù)
\( \Rightarrow \widehat {ECF} = {90^0}\)
Trong tứ giác CEDF, ta có:
\(\eqalign{
& \widehat {DEC} + \widehat {EDF} + \widehat {DFC} + \widehat {ECF} = {360^0} \cr
& \Rightarrow \widehat {DFC} = {360^0} – \left( {\widehat {DEC} + \widehat {EDF} + \widehat {ECF}} \right) \cr
& \widehat {DFC} = {360^0} – \left( {{{105}^0} + {{90}^0} + {{90}^0}} \right) = {75^0} \cr} \)
Câu 9: Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.
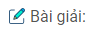
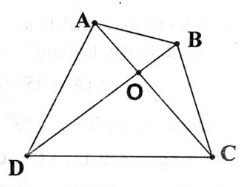
Gọi O là giao điểm của hai đường chéo AC và BD.
Trong ∆OAB, ta có:
OA + OB > AB (bất đẳng thức tam giác) (1)
Advertisements (Quảng cáo)
Trong ∆OCD, ta có:
OC + OD > CD (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2):
OA + OB + OC + OD > AB + CD
⇒ AC + BD > AB + CD
Câu 10: Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.
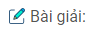
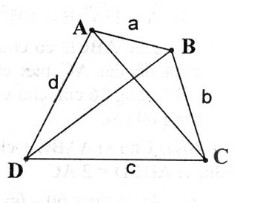
Đặt độ dài AB = a, BC = b, CD = c, AD = d
Gọi O là giao điểm hai đường chéo AC và BD
Trong ∆OAB, ta có:
OA + OA > a (bất đẳng thức tam giác) (1)
Trong ∆OCD ta có:
Từ (1) và (2) suy ra:
OA + OB + OC + OD > a + c
Hay AC + BD > a + c (*)
-Trong ∆OAD ta có: OA + OD > d (bất đẳng thức tam giác) (3)
-Trong ∆OBC ta có: OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra: OA + OD + OB + OC > b + d
⇒ AC + BD > b + d (**)
Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d
\(⇒ AC + BD > {{a + b + c + d} \over 2}\)
-Trong ∆ABC ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
-Trong ∆ADC ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra: 2AC < a + b + c + d
\(AC < {{a + b + c + d} \over 2}\) (5)
-Trong ∆ABD ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
-Trong ∆BCD ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra: 2BD < a + b + c + d
\(BD < {{a + b + c + d} \over 2}\) (6)
Từ (5) và (6) suy ra: AC + BD < a + b + c + d

