Câu 38: Cho tam giác ABC có AB = 10cm, AC = 20cm. Trên cạnh AC, đặt đoạn thẳng AD = 5cm.
Chứng minh \(\widehat {ABD} = \widehat {ACB}\).
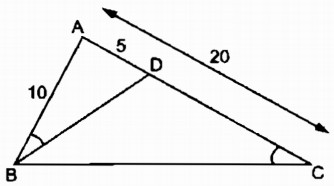
Ta có:
\(\eqalign{ & {{AD} \over {AB}} = {5 \over {10}} = {1 \over 2} \cr & {{AB} \over {AC}} = {{10} \over {20}} = {1 \over 2} \cr} \)
Suy ra: \({{AD} \over {AB}} = {{AB} \over {AC}}\)
Xét ∆ ADB và ∆ ABC, ta có:
\(\widehat A\) chung
\({{AD} \over {AB}} = {{AB} \over {AC}}\) (chứng minh trên )
Suy ra: ∆ ADB đồng dạng ∆ ABC (c.g.c)
Vậy \(\widehat {ABD} = \widehat {ACB}.\)
Câu 6.1: Hình bs.4 cho biết Oz là phân giác của góc xOy, OA = 9cm, OB = 12cm, OC = 16cm, AB = 6cm.
Advertisements (Quảng cáo)
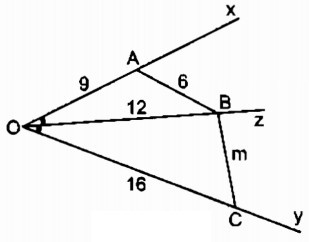
Độ dài của đoạn thẳng BC là m bằng:
A. 7,5cm
B. 8cm
C. 8,5cm
D. 9cm
Hãy chọn kết quả đúng.
Advertisements (Quảng cáo)
Chọn B
Câu 6.2: Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB.
a. Vẽ trung tuyến BE của tam giác ABO. Chứng minh rằng \(\widehat {ABE} = \widehat {ACB}\).
b. Gọi M là trung điểm của cạnh BC, chứng minh rằng EM vuông góc với đường chéo BD.
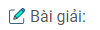
a. Vì ABCD là hình bình hành và E là trung điểm của AO (vì BE là trung tuyến của tam giác ABO) nên ta có:
\(\eqalign{ & AO = CO = {1 \over 2}AC; \cr & AE = {1 \over 2}AO. \cr} \)
Mặt khác, theo giả thiết AC = 2AB nên dễ thấy AB = AO và do đó \(AE = {1 \over 2}AB\)
Xét hai tam giác AEB và ABC, ta có:
Góc A chung
\({{AE} \over {AB}} = {{AB} \over {AC}} = {1 \over 2}\)
Vậy ∆ AEB đồng dạng ∆ ABC (c.g.c)
Suy ra: hai góc tương ứng bằng nhau \(\widehat {ABE} = \widehat {ACB}\) (đpcm)
b. Theo chứng minh ở câu a. ∆ AEB đồng dạng ∆ ABC theo tỉ số k = \({1 \over 2}\) nên dễ thấy \(BE = {1 \over 2}BC\) hay BE = BM
Suy ra: ∆ BEM cân tại B.
Xét tam giác EBC có:
\({{BE} \over {BC}} = {{OE} \over {OC}} = {1 \over 2}\)
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).

