Câu 5: Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E (hình dưới)
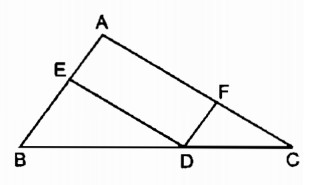
Chứng minh rằng :
\({{AE} \over {AB}} + {{AF} \over {AC}} = 1\)
(xem hình 4)

Trong ∆ ABC ta có: DE // AC (gt)
Suy ra: \({{AE} \over {AB}} = {{CD} \over {CB}}\) (định lí Ta-lét) (1)
Lại có: DF // AB (gt)
Suy ra: \({{AF} \over {AC}} = {{BD} \over {BC}}\) (định lí Ta-lét) (2)
Cộng trừ vế (1) và (2), ta có:
Advertisements (Quảng cáo)
\({{AE} \over {AB}} + {{AF} \over {AC}} = {{CD} \over {CB}} + {{BD} \over {BC}} = {{CD + BD} \over {BC}} = {{BC} \over {BC}} = 1\)
Câu 1.1: Hai đoạn thẳng AB = 35cm, CD = 105cm tỉ lệ với hai đoạn thẳng A’B’ = 75cm và C’D’
Đoạn thẳng C’D’ có độ dài (theo đơn vị cm) là :
A. 25
B. 49
C. 225
D. 315
Advertisements (Quảng cáo)
Hãy chọn kết quả đúng
Chọn C
Câu 1.2: Tam giác ABC vuông tại A có đường cao là AD (D ∈ BC). Từ D, kẻ DE vuông góc với AB (E ∈ AB) và DF vuông góc với AC (F ∈ AC).
Hỏi rằng, khi độ dài các cạnh AB, AC thay đổi thì tổng \({{AE} \over {AB}} + {{AF} \over {AC}}\) có thay đổi hay không ? Vì sao?.
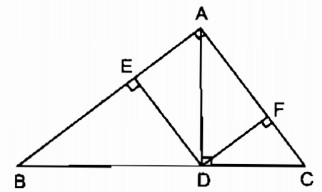
DE và CA cùng vuông góc với AB, do đó
DE // AC.
Theo định lí Ta-lét, ta có:
\({{AE} \over {AB}} = {{CD} \over {CB}}\) (1)
Tương tự, ta có: DF // AB, do đó:
\({{AF} \over {AC}} = {{BD} \over {BC}}\) (2)
Cộng các vế tương ứng của (1) và (2), ta có:
\({{AE} \over {AB}} + {{AF} \over {AC}} = {{CD} \over {CB}} + {{BD} \over {BC}} = {{CD + BD} \over {BC}} = {{BC} \over {BC}} = 1\)
Tổng \({{AE} \over {AB}} + {{AF} \over {AC}}\) không thay đổi vì luôn có giá trị bằng 1.
Vậy : Khi độ dài cạnh góc vuông AB, AC của tam giác vuông ABC thay đổi thì tổng \({{AE} \over {AB}} + {{AF} \over {AC}}\) luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.

