Câu 2.3: Cho a là số bất kì, hãy đặt dấu “<, >, ≤, ≥” vào ô vuông cho đúng
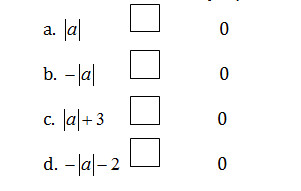
a. Dấu “≥” (xét khi a = 0 và a ≠ 0)
b. Dấu “≤”
c. Dấu “<”
– Nếu a = 0, ta có \(\left| a \right| = 0\)
Khi đó \(\left| a \right| + 3 = 3\)
– Nếu a ≠ 0, ta có \(\left| a \right| > 0\) , suy ra \(\left| a \right| + 3 > 3\) (1)
Với 3 và 0, ta có 3 > 0 (2)
Từ (1) và (2), theo tính chất bắc cầu ta có \(\left| a \right| + 3 > 0\)
Advertisements (Quảng cáo)
Kết luận: \(\left| a \right| + 3 > 0\)với a bất kì.
d. Dấu “<”
Câu 2.4

Câu 2.5
a. Cho x > 0, chứng tỏ
Advertisements (Quảng cáo)
\(x + {1 \over 2} \ge 2\)
b. Từ kết quả câu a, nếu x < 0 sẽ có kết quả nào ?
a. Nếu có \(x + {1 \over 2} \ge 2\) thì suy ra \(x + {1 \over x} \ge 2\)
nên ta sẽ chứng tỏ \(x + {1 \over x} – 2 \ge 0\)
Ta có, \(x + {1 \over x} – 2 = {{{x^2} + 1 – 2x} \over x} = {{{{\left( {x – 1} \right)}^2}} \over x}\)
Vì \({\left( {x – 1} \right)^2} \ge 0\) với x bất kì và x > 0 nên \({{{{\left( {x – 1} \right)}^2}} \over x} \ge 0\)
Vậy \(x + {1 \over x} – 2 \ge 0\) , nghĩa là \(x + {1 \over x} \ge 2\)
b. Nếu x < 0, ta đặt a = -x thì a > 0
Từ kết quả câu a, ta có \(a + {1 \over a} \ge 2\)
Thay a = -x, ta có:
\( – x = {1 \over { – x}} \ge 2\) (1)
Nhân hai vế của (1) với số -1, ta có:
\(x + {1 \over x} \le – 2\)
Vậy, với x < 0 thì \(x + {1 \over x} \le – 2\)

