Câu 2.1: a. Nền của một phòng học có dạng hình chữ nhật, với chiều rộng đo được là 4m và chiều dài là 6m. Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là 33,33cm ?
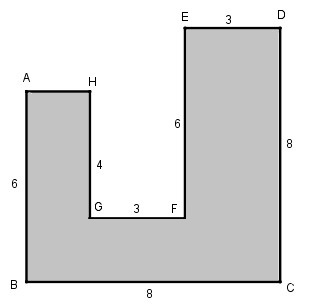
b. Cần bao nhiêu viên gạch có hình vuông, với cạnh là 25cm để có thể lát kín một mảnh sân có dạng như hình bs. 23 (biết AB = 6cm, BC = 8m, CD = 8m, DE = 3m, EF = 6m, FG = 3m, GH = 4m và góc tại các đỉnh A, B, C, D, E, F, G, H đều là góc vuông) ?

a. Diện tích nền phòng học : 4.6 = 24 (\({m^2}\))
b. Số viện gạch cần dùng : 24 : (0.3333) 216 (viên)
Câu 2.2: a. Dùng diện tích để chứng tỏ : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)
b. Dùng diện tích để chứng tỏ : \({\left( {a – b} \right)^2} = {a^2} – 2ab + {b^2}\)với điều kiện b < a


a. Dựng hình vuông ABCD có cạnh bằng (a + b )
Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F.
Ta có : diện tích hình vuông ABCD bằng \({\left( {a + b} \right)^2}\)
Diện tích hình vuông DKFG bằng \({a^2}\)
Advertisements (Quảng cáo)
Diện tích hình chữ nhật AKFE bằng a.b
Diện tích hình vuông EBHF bằng \({b^2}\)
Diện tích hình chữ nhật HCGF bằng a.b
\({S_{ABCD}} = {S_{DKFG}} + {S_{AKFE}} + {S_{EBHF}} + {S_{HCGF}}\)
Vậy ta có : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)
b. Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Advertisements (Quảng cáo)
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng \({a^2}\)
Hình vuông DKFG có diện tích bằng \({\left( {a – b} \right)^2}\)
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng \({b^2}\)
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
\({S_{ABCD}} = {S_{DKFG}} + {S_{AEFK}} = {S_{EBHF}} + {S_{HCGF}}\)
nên \({\left( {a – b} \right)^2} + \left( {a – b} \right)b + \left( {a – b} \right)b + {b^2} = {a^2}\)
\(\Rightarrow {\left( {a – b} \right)^2} = {a^2} – 2ab + {b^2}\)
Câu 2.3: Đố vui
a. Có thể dùng kéo cắt một lần và chỉ cắt theo đường thẳng, chia một hình chữ nhật thành hai mảnh để ghép lại được một tam giác vuông hay không ?
b. Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thằng, chai một hình chữ nhật thành ba mảnh để ghép lại được một tam giác thường hay không ?

a. Ta có thể cắt ghép như hình vẽ bên.

b. Ta có thể cắt ghép như hình bên dưới.


