Câu 46: Cho bán kính của Trái Đất và Mặt Trăng tương ứng là 6371 và 1738 kilomet. Trong các số sau đây, số nào là tỉ số thể tích giữa Trái Đất và Mặt Trăng?
(A) 3.67 (C) 15,63
(B) 4,93 (D) 49,26
Thể tích trái đất: \({V_1} = {4 \over 3}\pi {.6371^3}\)
Thể tích của mặt trăng: \({V_2} = {4 \over 3}\pi {.1738^3}\)
\({V_1}:{V_2} = {{{{6371}^3}} \over {{{1738}^3}}} = {\left( {{{6371} \over {1738}}} \right)^3} \approx 49,26\)
Chọn (D) 49,26
Câu 47: Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h
a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h (cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu?
b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu?
a) Thể tích nửa hình cầu bán kính 12 cm là:
Advertisements (Quảng cáo)
\(V = {1 \over 2}.{4 \over 3}\pi {.12^3} = 1152\pi \left( {c{m^3}} \right)\)
Bán kính đáy hình trụ: \(r = {h \over 2}\)
Thể tích hình trụ: \(V = \pi {r^2}.h\)
\(\eqalign{
& V = \pi .{\left( {{h \over 2}} \right)^2}.h = {1 \over 4}\pi .{h^3} \cr
& \Rightarrow {1 \over 4}\pi .{h^3} = 1152\pi \cr
& \Rightarrow {h^3} = 4608 \cr
& h = \root 3 \of {4608} \approx 16,64\left( {cm} \right) \cr} \)
Câu 48: Hình bên (h.113) gồm một hình nón được đặt khít vào bên trong một cốc hình trụ, chúng có cùng đáy, cùng chiều cao. Người ta đổ vào đó một lượng nước lên đến một nửa chiều cao của hình. (Giả sử rằng nước không rò rỉ, không thẩm thấu vào bên trong hình nón)
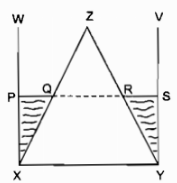
Hãy chọn đúng tỉ số giữa các đoạn thẳng \({{QR} \over {XY}}\)
(A) \({1 \over 2}\);
Advertisements (Quảng cáo)
(B) \({1 \over 3}\);
(C) \({2 \over 3}\)
(D) Không tính được, vì câu hỏi phụ thuộc vào bán kính đáy.
Vì hình trụ và hình nón có cùng chiều cao, người ta đổ nước lên đến nửa chiều cao của hình nên Q là trung điểm của xz, R là trung điểm của yz
Nên \({{QR} \over {XY}} = {1 \over 2}\)
Chọn (A) \({1 \over 2}\).
Câu 49: Hai cái lọ có dạng hình trụ, các kích thước như ở hình 114. Lọ nào có dung tích lớn hơn?
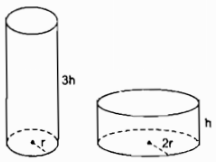
Thể tích của hình trụ có bán kính đáy là r
\({V_1} = \pi {r^2}.3h = 3\pi {r^2}h\) (đơn vị thể tích)
Thể tích của hình trụ có bán kính đáy 2r
\({V_2} = \pi {\left( {2r} \right)^2}.h = 4\pi {r^2}h\) (đơn vị thể tích)
Dung tích hình trụ cao nhỏ hơn dung tích hình trụ thấp.

