Câu 31: Hai hình cầu A và B có các bán kính tương ứng là x và 2x (cm)
Tỉ số các thể tích của 2 hình cầu này là:
(A) 1: 2
(B) 1: 4
(C) 1: 8
(D) Một kết quả khác
Hãy chọn kết quả đúng
 :
:
Hình cầu A có bán kính r = x có thể tích: \({V_1} = {4 \over 3}\pi {x^3}\left( {c{m^3}} \right)\)
Hình cầu B có bán kính r = 2x có thể tích: \({V_2} = {4 \over 3}\pi {\left( {2x} \right)^3} = {{32} \over 3}\pi {x^3}\left( {c{m^3}} \right)\)
\({V_1}:{V_2} = {4 \over 3}:{{32} \over 3} = {4 \over 3}.{3 \over {32}} = {1 \over 8}\)
Chọn (C) 1: 8
Câu 32: Hình 105 minh họa: hình gồm một nửa hình cầu và một hình nón
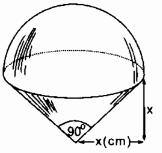
Thể tích của hình nhận giá trị nào trong các giá trị sau:
(A) \({2 \over 3}\pi {x^3}(c{m^3})\)
(B) \(\pi {x^3}(c{m^3})\)
(C) \({4 \over 3}\pi {x^3}(c{m^3})\)
(D) \(2\pi {x^3}(c{m^3})\)
 :
:
Hình gồm một nửa hình cầu có bán kính là x và một hình nón có bán kính đáy bằng x, chiều cao bằng x.
Thể tích nửa hình cầu: \({V_1} = {1 \over 2}.{4 \over 3}\pi {x^3} = {2 \over 3}\pi {x^3}(c{m^3})\)
Thể tích của hình nón: \({V_2} = {1 \over 3}\pi .{x^2}.x = {1 \over 3}\pi {x^3}(c{m^3})\)
Tổng thể tích của 2 hình đó là: \({2 \over 3}\pi {x^3} + {1 \over 3}\pi {x^3} = \pi {x^3}(c{m^3})\)
Chọn (B) \(\pi {x^3}(c{m^3})\)
Câu 33: Một quả bóng hình cầu bên trong một hình lập phương như hình 106
Advertisements (Quảng cáo)
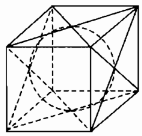
a) Tính tỉ số giữa diện tích toàn phần của hình lập phương với diện tích mặt cầu
b) Nếu diện tích mặt cầu là \(7\pi (c{m^2})\) thì diện tích toàn phần của hình lập phương là bao nhiêu?
c) Nếu bán kính hình cầu là 4cm thì thể tích phần trống (trong hình hộp ngoài hình cầu) là bao nhiêu?
Gọi cạnh hình lập phương là a thì bán kính cầu \(r = {a \over 2}\)
a) Diện tích toàn phần của hình lập phương: \({S_1} = 6{a^2}\) (đơn vị diện tích)
Diện tích mặt cầu: \({S_2} = 4.\pi .{\left( {{a \over 2}} \right)^2} = 4\pi .{{{a^2}} \over 4} = \pi {a^2}\) (đơn vị diện tích)
Tỉ số \({S_1}:{S_2} = 6{a^2}:\pi {a^2} = {6 \over \pi }\)
b) Diện tích mặt cầu \(7\pi (c{m^2})\) ta có: \({S_1}:7\pi = {6 \over \pi }\)
\( \Rightarrow {S_1} = {6 \over \pi }.7\pi = 42\) \(\left( {c{m^2}} \right)\)
c) Bán kính hình cầu r = 4cm thì cạnh hình lập phương 2r = 8cm
Thể tích của hình lập phương: \({V_1} = {a^3} = {8^3} = 512\left( {c{m^3}} \right)\)
Thể tích hình cầu: \({V_2} = {4 \over 3}\pi {r^3} = {4 \over 3}\pi {.4^3} = {{256} \over 3}\pi \left( {c{m^3}} \right)\)
Thể tích hình lập phương nằm ngoài hình cầu:
\(V = {V_1} – {V_2} = 512 – {{256} \over 3}\pi \approx 243,717\left( {c{m^3}} \right)\)
Advertisements (Quảng cáo)
Câu 34: Sử dụng các thông tin và hình 107 để trả lời các câu hỏi sau:
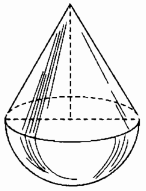
Mooth đồ chơi “lắc lư” của trẻ em gồm một hình nón gắn với nửa hình cầu (h.107) (chiều cao của hình nón bằng đường tròn đáy). Có hai loại đồ chơi: loại thứ nhất cao 9cm, loại thứ hai cao 18cm
a) Tỉ số: \({{thetichdochoiloaithuhai} \over {thetichdochoiloaithunhat}}\)
(A) 2 (C) 8
(B) 4 (D) 16
Hãy chọn kết quả đúng.
b) Trong các số sau đây:
(A) 2 (cm) (C) 4 (cm)
(B) 3 (cm) (D) \(4{1 \over 2}\) (cm)
Số nào là bán kính đường tròn đáy của đồ chơi loại thứ nhất?
c) Trong các số sau đây:
(A) \(30\pi \left( {c{m^3}} \right)\)
(B) \(36\pi \left( {c{m^3}} \right)\)
(C) \(36\pi \left( {c{m^3}} \right)\)
(D) \(610\left( {c{m^3}} \right)\)
Số nào là thể tích của loại đồ chơi thứ nhất?
a) Loại thứ nhất có chiều cao 9cm là bao gồm chiều cao của hình nón và bán kính của hình cầu, mà chiều cao hình nón bằng đường kính hình cầu
Suy ra: \(2r + r = 9 \Rightarrow r = 3\left( {cm} \right)\)
Chiều cao hình nón: h = 6cm
Thể tích hình nón: \({V_1} = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {.3^2}.6 = 18\pi \left( {c{m^3}} \right)\)
Thể tích nửa hình cầu: \({V_2} = {1 \over 2}.{4 \over 3}\pi {.3^3} = 18\pi \left( {c{m^3}} \right)\)
Thể tích loại thứ nhất là \(36\pi \left( {c{m^3}} \right)\)
Loại thứ 2 có chiều cao 18cm là bao gồm chiều cao hình nón và bán kính hình cầu mà chiều cao hình nón bằng đường kính hình cầu.
Suy ra: \(2r + r = 18 \Rightarrow r = 6\)
Chiều cao hình nón: h = 12cm
Thể tích hình nón: \({V_1}’ = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {.6^2}.12 = 144\pi \left( {c{m^3}} \right)\)
Thể tích nửa hình cầu: \({V_2}’ = {1 \over 2}.{4 \over 3}\pi {r^3} = {1 \over 2}.{4 \over 3}\pi {.6^3} = 144\pi \left( {c{m^3}} \right)\)
Thể tích loại thứ 2 là: \(288\pi \left( {c{m^3}} \right)\)
\({{thetichloaithuhai} \over {thetichloaithunhat}} = {{288\pi } \over {36\pi }} = 8\)
Chọn (C) 8
b) Bán kính đường tròn đáy đồ chơi thứ nhất
Chọn (B) 3cm
c) Thể tích đồ chơi thứ nhất
Chọn (B) \(36\pi \left( {c{m^3}} \right)\).

