Câu 42: Độ dài các cạnh của một tam giác ABC vuông tại A, thỏa mãn các hệ thức sau
BC = AB + 2a (1)
\(AC = {1 \over 2}\left( {BC + AB} \right)\) (2)
a là một độ dài cho trước
a) Tính theo a, độ dài các cạnh và chiều cao AH của tam giác
b) Tam giác ABC nội tiếp được trong nửa hình tròn tâm O. Tính diện tích của phần thuộc nửa đường tròn nhưng ở ngoài tam giác đó
c) Cho tam giác ABC quay một vòng quanh cạnh huyền BC. Tính tỉ số diện tích giữa các phần do các dây cung AB và AC tạo ra
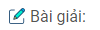
a) Đặt độ dài cạnh AB = x; điều kiện: x > 0
Theo bài ra theo điều (1) ta có: BC = x + a (3)
Từ (2) và (3) \( \Rightarrow AC = {1 \over 2}\left( {x + 2a + x} \right) = x + a\)
\(\Delta ABC\) vuông tại A, theo định lí Pitago ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
\(\eqalign{
& \Rightarrow {\left( {x + 2a} \right)^2} = {x^2} + {\left( {x + a} \right)^2} \cr
& \Leftrightarrow {x^2} + 4ax + 4{a^2} = {x^2} + {x^2} + 2ax + {a^2} \cr
& \Leftrightarrow {x^2} – 2ax – 3{a^3} = 0 \cr
& \Delta = {\left( { – 2a} \right)^2} – 4.1\left( { – 3{a^2}} \right) = 4{a^2} + 12{a^2} = 16{a^2} > 0 \cr
& \Rightarrow \sqrt \Delta = \sqrt {16{a^2}} = 4a \cr
& {x_1} = {{2a + 4a} \over {2.1}} = {{6a} \over 2} = 3a \cr
& {x_2} = {{2a – 4a} \over {2.1}} = – a \cr} \)
Vì x > 0 \( \Rightarrow {x_2} = – a\) (loại)
Vậy cạnh AB = 3a; AC = 3a + a = 4a; BC = 3a + 2a =5a
AH.BC = AB.AC
\( \Rightarrow {\rm A}{\rm H} = {{AB.AC} \over {BC}} = {{3a.4a} \over {5a}} = {{12a} \over 5}\)
b) Diện tích của \(\Delta ABC\):
\({S_1} = {1 \over 2}AB.AC = {1 \over 2}.3a.4a = 6{a^2}\) (đơn vị diện tích)
\(\Delta ABC\) nội tiếp trong (O) bán kính đường tròn: \(R = {{BC} \over 2} = {{5a} \over 2}\)
Diện tích nửa hình tròn: \({S_2} = {1 \over 2}\pi .{r^2} = {1 \over 2}\pi .{\left( {{{5a} \over 2}} \right)^2} = {{25\pi {a^2}} \over 8}\)
Phần diện tích nửa hình tròn nằm ngoài tam giác:
Advertisements (Quảng cáo)
\(S = {S_2} – {S_1} = {{25\pi {a^2}} \over 8} – 6{a^2} = {{{a^2}} \over 8}\left( {25\pi – 48} \right)\)
c) Khi quay \(\Delta ABC\) một vòng quanh cạnh BC thì AB và AC vạch nên hai hình nón có bán kính đáy là AH.
Diện tích phần do dây cung AB tạo ra:
\({S_1} = \pi .AH.AB = \pi .AH.3a\)
Diện tích phần do dây cung cung AC tạo ra
\(\eqalign{
& {S_2} = \pi .AH.AC = \pi AH.3a \cr
& {{{S_1}} \over {{S_2}}} = {{\pi .AH.3a} \over {\pi .AH.4a}} = {3 \over 4} \cr} \)
Câu 43: Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:
a) Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 \(\left( {c{m^2}} \right)\)
b) Thể tích hình nón, biết thể tích hình cầu là 15,8 \(\left( {c{m^3}} \right)\)
a) Đường sinh của hình nón:
\(\eqalign{
& A{B^2} = A{H^2} + B{H^2} = 4{r^2} + {r^2} = 5{r^2} \cr
& AB = r\sqrt 5 \cr} \)
Diện tích toàn phần hình nón:
Advertisements (Quảng cáo)
\(\eqalign{
& {S_{TP}} = {S_{xq}} + {S_{day}} = \pi .r.r\sqrt 5 + \pi {r^2}\left( {\sqrt 5 + 1} \right) \cr
& {S_{TP}} = 21,06 \Rightarrow \pi {r^2}\left( {\sqrt 5 + 1} \right) = 21,06 \cr
& \Rightarrow {r^2} = {{21.06} \over {\pi \left( {\sqrt 5 + 1} \right)}} \cr} \)
Diện tích mặt cầu:
\(\eqalign{
& S = 4\pi {r^2} \cr
& S = 4\pi .{{21,06} \over {\pi \left( {\sqrt 5 + 1} \right)}} = 21.06\left( {\sqrt 5 – 1} \right) \approx 26,03\left( {c{m^2}} \right) \cr} \)
b) Thể tích hình cầu: \(V = {4 \over 3}\pi {r^3}\)
Thể tích bằng \(15,8c{m^3} \Rightarrow {4 \over 3}\pi {r^3} = 47,4 \Rightarrow {r^3} = {{47,4} \over {4\pi }} = {{23,7} \over {2\pi }}\)
Thể tích hình nón:
\(\eqalign{
& V = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {r^2}.2r = {2 \over 3}\pi {r^3} \cr
& \Rightarrow V = {2 \over 3}\pi .{{23,7} \over {2\pi }} = {{23,7} \over 3} = 7,9\left( {c{m^3}} \right) \cr} \)
Câu 44: Một cái hộp hình trụ được làm ra sao cho một quả bóng hình cầu đặt vừa khít vào hộp đó (h.111)
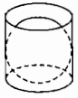
Tỉ số \({{{V_{cau}}} \over {{V_{tru}}}}\) là:
(A) \({3 \over 4}\) (C) \({3 \over 2}\)
(B) \({4 \over 3}\) (D) \({2 \over 3}\)
Hãy chọn kết quả đúng.
Hình cầu đặt khít trong hình trụ nên bán kính hình cầu bằng bán kính đáy hình trụ, chiều cao hình trụ bằng đường kính hình cầu
Thể tích hình trụ: \({V_1} = \pi .{r^2}.h = \pi {r^2}.2r = 2\pi {r^3}\)
Thể tích hình cầu: \({V_2} = {4 \over 3}\pi {r^3}\)
\({V_2}:{V_1}\)
Chọn (D) \({2 \over 3}\)
Câu 45: Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính:
a) Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.
b) Thể tích hình cầu.
c) Diện tích mặt cầu.
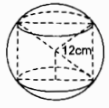
a) Đường chéo mặt cắt hình trụ đi qua trục là đường kính của hình cầu. Hình trụ có đường cao bằng đường kính đáy bằng \(12\sqrt 2 \left( {cm} \right)\)
Diện tích xung quanh hình trụ:
\(\eqalign{
& {S_{xq}} = 2\pi r.h \cr
& {S_{xq}} = \pi .12\sqrt 2 .12\sqrt 2 = 288\pi \left( {c{m^2}} \right) \cr} \)
b) Thể tích hình cầu:
\(V = {4 \over 3}\pi {.12^3} = 2304\left( {c{m^3}} \right)\)
c) Diện tích mặt cầu:
\(S = 4\pi {.12^2} = 576\pi \left( {c{m^3}} \right)\)

