Câu 39: Với một cái thước dây, liệu có thể xác định được thể tích của một vật thể có dạng hình cầu hay không?
Dùng thước dây tạo ra đường tròn đặt vừa khít hình cầu, ta có độ dài của đường tròn lớn hơn là \(C \Rightarrow r = {C \over {2\pi }}\)
Thể tích: \(V = {4 \over 3}\pi {\left( {{C \over {2\pi }}} \right)^3} = {4 \over 3}\pi .{{{C^3}} \over {8{\pi ^3}}} = {{{C^3}} \over {6{\pi ^2}}}\)
Câu 40: Chiều cao của một hình trụ gấp ba lần bán kính đáy của nó. Tỉ số của thể tích hình trụ này và thể tích của hình cầu có bán kính bằng bán kính đáy của hình trụ là
(A) \({4 \over 3}\) (C) \({3 \over 1}\)
(B) \({9 \over 4}\) (D) \({4 \over 9}\)
Hãy chọn kết quả đúng.
Advertisements (Quảng cáo)
Thể tích của hình trụ: \({V_1} = \pi {r^2}.h = \pi {r^2}.3r = 3\pi {r^3}\)
Thể tích của hình cầu: \({V_2} = {4 \over 3}\pi {r^3}\)
Ta có: \({V_1}:{V_2}\)
Chọn (B) \({9 \over 4}\)
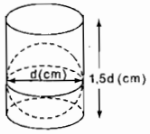
Câu 41: Một hình cầu đường kính d (cm) được đặt vào trong một hình trụ có chiều cao là 1,5d (cm) như hình 110. Xét các phân số sau đây
Advertisements (Quảng cáo)
(A) \({2 \over 3}\) (C) \({2 \over 9}\)
(B) \({4 \over 9}\) (D) \({1 \over 3}\)
Đâu là tỉ số \({{{V_{cau}}} \over {{V_{tru}}}}\)
Thể tích của hình trụ: \({V_1} = \pi {r^2}.h = \pi {r^2}.3r = 3\pi {r^3}\)
Thể tích của hình cầu: \({V_2} = {4 \over 3}\pi {r^3}\)
Thể tích của hình cầu: \({V_2} = {4 \over 3}\pi {r^3} = {4 \over 3}\pi {\left( {{d \over 2}} \right)^3} = {4 \over 3}\pi .{{{d^3}} \over 8} = {1 \over 6}\pi {d^3}\)
Ta có: \({V_2}:{V_1}\)
Chọn (B) \({4 \over 9}\)

