Câu 6.1: Hãy nối mỗi cột của ô bên trái với một ô của cột bên phải để được khẳng định đúng.
|
1. Trục đối xứng của tam giác ABC (AB = BC) là |
A. đường trung trực của AB. |
|
2. Trục đối xứng của hình thang cân ABCD (AB // CD) là |
B. đường trung trực của BC. |
|
|
C. đường trung trực của AC. |
Nối 1. với B
Nối 2. với A
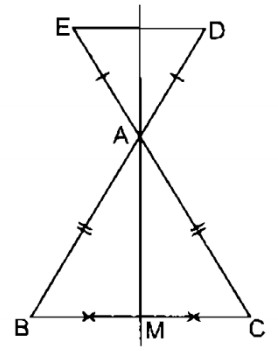
Câu 6.2: Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Gọi M là trung điểm của BC. Chứng minh rằng D đối xứng với E qua AM.
Advertisements (Quảng cáo)
∆ ABC cân tại A
AM là đường trung tuyến
⇒ AM là tia phân giác \(\widehat {BAC}\)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {BAM} = \widehat {MAC}\) (1)
Kéo dài MA cắt DE tai N, ta có:
\(\widehat {BAM} = \widehat {DAN}\) (đối đỉnh) (2)
\(\widehat {MAC} = \widehat {NAE}\) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: \(\widehat {DAN} = \widehat {NAE}\)
∆ ADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.

