Câu 5.1: Dựng hình thang cân ABCD(AB // CD) biết BC = 3cm, AC = 2cm, đường cao bằng 2,5cm.


Cách dựng:
– Dựng ∆ BHC, BH = 2,5 cm
– \(\widehat {BHC} = {90^0}\)
– BC = 3cm
– Dựng tia đi qua B và song song CH nằm trên nửa mặt phẳng bờ BC chứa điểm H. Lấy điểm A sao cho BA = 2cm
Advertisements (Quảng cáo)
– Dựng cung tròn tâm B bán kính bằng AC cắt đường thẳng CH tại D.
Nối AD ta có hình thang ABCD cần dựng.
Chứng minh: Thật vậy theo cách dựng AB // CD nên tứ giác ABCD là hình thang có AB = 2cm, BC = 3cm, BH = 2,5cm.
AC = BD
Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.
Advertisements (Quảng cáo)
Câu 5.2: Dựng tam giác ABC biết \(\widehat B = {80^0}\), BC = 3cm, AB + AC = 5cm.

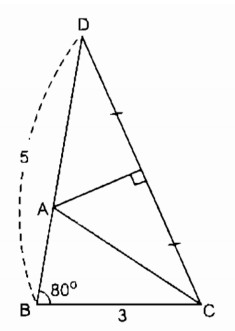
Cách dựng:
– Dựng tam giác ABC có \(\widehat B = {80^0}\), BC = 3cm, BD = 5cm.
– Dựng I là trung điểm của CD
– Dựng đường trung trực CD cắt BD tại A
Nối A với C ta có ∆ ABC cần dựng
Chứng minh: Thật vậy theo cách dựng ta có ∆ ABC
\(\widehat B = {80^0}\), BC = 3cm, AB + AC = AB + AD (vì AC = AD tính chất đường trung trực nên AB + AC = 5 cm)
∆ ABC thỏa mãn điều kiện bài toán.

