Câu 22: Hình thang cân ABCD có AB// CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng DH = CK.
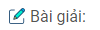
Xét hai tam giác vuông AHD và BKC:
\(\widehat {AHD} = \widehat {BKC} = {90^0}\)
AD=BC (tính chất hình thang cân)
\(\widehat C = \widehat D\) (gt)
Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
Câu 23: Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA=OB, OC=OD.

Xét ∆ ADC và ∆ BCD, ta có:
AD = BC (tính chất hình thang cân)
\(\widehat {ADC} = \widehat {BCD}\) (gt)
DC cạnh chung
Do đó: ∆ ADC = ∆ BCD (c.g.c)
\( \Rightarrow {\widehat C_1} = {\widehat D_1}\)
Advertisements (Quảng cáo)
Trong ∆ OCD ta có: \({\widehat C_1} = {\widehat D_1}\)
⇒ ∆ OCD cân tại O
⇒ OC = OD (1)
AC = BD ( tính chất hình thang cân)
⇒ AO + OC = BO + OD (2)
Từ (1) và (2) suy ra: AO = BO
Câu 24: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a. Tứ giác BMNC là hình gì ? Vì sao ?
b. Tính các góc của tứ giác BMNC biết rằng \(\widehat A = {40^0}\)
Advertisements (Quảng cáo)
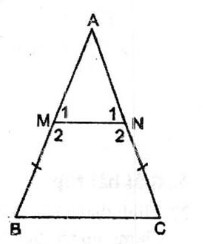
a. ∆ ABC cân tại A
\( \Rightarrow \widehat B = \widehat C = {{{{180}^0} – \widehat A} \over 2}\) (tính chất tam giác cân) (1)
AB = AC (gt)
⇒ AM + BM= AN+ CN
⇒ mà BM = CN (gt)
⇒ suy ra: AM = AN
⇒ ∆ AMN cân tại A
\( \Rightarrow {\widehat M_1} = {\widehat N_1} = {{{{180}^0} – \widehat A} \over 2}\) ( tính chất tam giác cân) (2)
⇒ Từ (1) và (2) suy ra: \({\widehat M_1} = \widehat B\)
⇒MN // BC ( vì có các cặp góc đồng vị bằng nhau)
Tứ giác BCMN là hình thang có \(\widehat B = \widehat C\). Vậy BCMN là hình thang cân.
b. \(\widehat B = \widehat C = {{{{180}^0} – \widehat A} \over 2} = {{{{180}^0} – {{40}^0}} \over 2} = {70^0}\)
Mà \({\widehat M_2} + \widehat B = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow {\widehat M_2} = {180^0} – \widehat B = {180^0} – {70^0} = {110^0}\)
\({\widehat N_2} = {\widehat M_2} = {110^0}\) (tính chất hình thang cân)
Câu 25: Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.
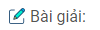
Xét hai tam giác AEB và AFC
Có AB = AC (∆ ABC cân tại A)
\(\widehat {ABE} = {{\widehat B} \over 2} = {{\widehat C} \over 2} = \widehat {ACF}\) và \(\widehat A\) là góc chung
\( \Rightarrow \Delta ADB = \Delta AEC\left( {g.c.g} \right) \Rightarrow AE = AF \Rightarrow \Delta AEF\) cân tại A
\( \Rightarrow \widehat {AFE} = {{{{180}^0} – \widehat A} \over 2}\) và trong tam giác \(\Delta ABC:\,\,\widehat B = {{{{180}^0} – \widehat A} \over 2}\)
\( \Rightarrow \widehat {AFE} = \widehat B \Rightarrow FE//BC\) ⟹ tứ giác BFEC là hình thang.

