Câu 45: Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
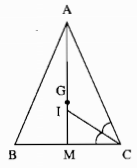
Kẻ đường phân giác của \(\widehat A\) và \(\widehat C\) cắt nhau tại I, AI cắt BC tại M.
∆ABC cân tại A.
Đường phân giác AM cũng là đường trung tuyến (tính chất tam giác cân)
G là trọng tâm của ∆ABC
\( \Rightarrow \) G ∈ AM
Vậy A, I, G thẳng hàng.
Câu 46: Cho tam giác ABC. Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đoạn thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất.
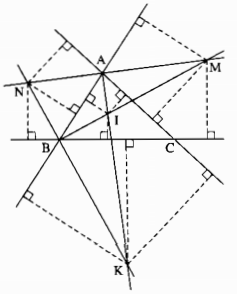
Nếu O là điểm nằm trong ∆ABC
Kẻ \(OH \bot AB,OK \bot BC,OI \bot {\rm{A}}C\)
Vì điểm O cách đều các đường thẳng AB, BC, CA.
\( \Rightarrow \) OH = OK = OI
Advertisements (Quảng cáo)
OH = OK
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {ABC}\)
OI = OK
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {ACB}\)
Vậy O là giao điểm các đường phân giác của ∆ABC.
Nếu O’ nằm ngoài ∆ABC
Kẻ \(O’D \bot AB,O’E \bot BC,O’F \bot {\rm{AC}}\)
\( \Rightarrow \) O’D = O’E = O’F
O’D = O’F
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {BAC}\)
Advertisements (Quảng cáo)
O’D = O’E
\( \Rightarrow \) O’ nằm trên tia phân giác \(\widehat {DBC}\)
\( \Rightarrow \) O’ là giao điểm phân giác trong của \(\widehat {BAC}\) và phân giác ngoài tại đỉnh D. nên A, O, O’ thẳng; A, H, D thẳng hàng.
Ta có: OH < O’D
Vậy O là giao điểm các đường phân giác trong của ∆ABC cách đều ba đường thẳng AB, BC, CA và ngắn nhất.
Câu 47: Tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh rằng tam giác đó là tam giác cân.
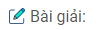
Kẻ \(MH \bot AB,MK \bot {\rm{A}}C\)
AM là tia phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) MH = MK (tính chất tia phân giác)
Xét hai tam giác vuông MHB và MKC:
\(\widehat {MHB} = \widehat {MKC} = 90^\circ \)
MH = MK (chứng minh trên)
MB = MC (gt)
Do đó: ∆MHB = ∆MKC (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \widehat B = \widehat C\)
Vậy ∆ABC cân tại A.
Câu 48: Cho tam giác ABC cân tại A. Các đường phân giác BD, CE cắt nhau ở K. Chứng minh rằng AK đi qua trọng điểm của BC.
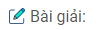
Các đường phân giác BD và CE cắt nhau tại K nên AK là đường phân giác của góc A.
Gọi M là trung điểm của BC.
Trong tam giác cân đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy.
Vậy AK đi qua trung điểm M của BC.

