Câu 31: Một bánh xe răng cưa có 24 răng (quay được 80 vòng trong 1 phút). Nó khớp với một bánh xe răng cưa khác có x răng. Giả sử bánh xe răng cưa thứ hai quay được y vòng trong 1 phút. Hãy biểu diễn y theo x.
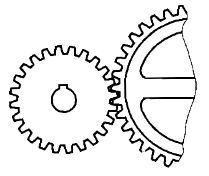
Vì số vòng quay và số răng cưa của hai bánh xe là hai đại lượng tỉ lệ nghịch với nhau, ta có:
$${\rm{x}}.y = 24.80 \Rightarrow y = {{1920} \over x}$$
Câu 32: Hai bánh xe nối với nhau bởi một dây tời (hình 4). Bánh xe lớn có bán kính 15cm, bánh xe nhỏ có bán kính 10cm. Bánh xe lớn quay được 30 vòng trong 1 phút. Hỏi bánh xe nhỏ quay được bao nhiêu vòng trong 1 phút?
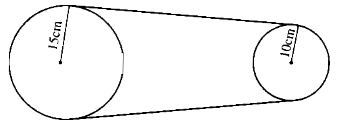
Gọi x (vòng) là số vòng quay bánh xe nhỏ trong 1 phút.
Trong cùng một đơn vị thời gian thì số vòng quay và chu vi của bánh xe là hai đại lượng tỉ lệ nghịch.
Advertisements (Quảng cáo)
Ta có: \({x \over {30}} = {{2\pi .15} \over {2\pi .10}} = {3 \over 2} \Rightarrow x = {{30.3} \over 2} = 45\) (vòng)
Vậy trong 1 phút bánh xe lớn quay 30 vòng thì bánh xe nhỏ quay 45 vòng.
Câu 33: Đố vui: Hai bạn Bình và Minh đi mua vở, mỗi bạn mang theo số tiền vừa đủ mua 20 quyển. Khi đến cửa hàng thấy vở bán hạ giá 20%, Bình cho rằng sẽ mua được 24 quyển (tăng thêm 20%) còn Minh lại bảo sẽ mua được 25 quyển (tăng 25%). Theo bạn: Ai đúng? Vì sao?
Bạn Minh đúng vì số tiền không đổi nên giá tiền của mỗi quyển và số quyển vở mua được là hai đại lượng tỉ lệ nghịch.
Advertisements (Quảng cáo)
Gọi x là giá tiền của một quyển vở ban đầu, y là số vở mua lúc sau.
Ta có: \(20.x = y.0,8{\rm{x}} \Rightarrow y = {{20.x} \over {0,8.x}} = 25\)
Câu 34: Hai xe máy cùng đi từ A đến B. Một xe đi hết 1 giờ 20 phút, xe kia đi hết 1 giờ 30 phút. Tính vận tốc trung bình của mỗi xe, biết rằng trung bình 1 phút xe thứ nhất đi hơn xe thứ hai 100m.
Ta có: 1 giờ 20 phút = 80 phút
1 giờ 30 phút = 90 phút
Gọi \({V_1},{V_2}\) lần lượt là vận tốc của xe đi 80 phút và xe đi 90 phút.
Vì quãng đường không đổi nên vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.
Ta có: \({V_1} = 90.{V_2}\) và \({V_1} – {V_2} = 100 \Rightarrow {{{V_1}} \over {90}} = {{{V_2}} \over {80}}\)
Theo tính chất dãy tỉ số bằng nhau, ta có:
\({{{V_1}} \over {90}} = {{{V_2}} \over {80}} = {{{V_1} – {V_2}} \over {90 – 80}} = {{100} \over {10}} = 10\)
\(\eqalign{
& {{{V_1}} \over {90}} = 10 \Rightarrow {V_1} = 10.90 = 900 \cr
& {{{V_2}} \over {80}} = 10 \Rightarrow {V_2} = 10.80 = 800 \cr} \)
Vậy vận tốc xe thứ nhất \({V_1} = 900\) (m/phút) = 54(km/h).
Vận tốc xe thứ hai \({V_2} = 800\) (m/phút) = 48(km/h).

