Câu 69: Vẽ trên cùng một hệ trục tọa độ của các hàm số:
a) y = x b) y = 2x c) y = -2x
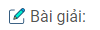
a) Vẽ đồ thị y = x.
Đồ thị đi qua O(0; 0). Cho x = 1 \( \Rightarrow \) y =1.
Ta có: A(1; 1). Vẽ đường thẳng OA ta có đồ thị hàm số.
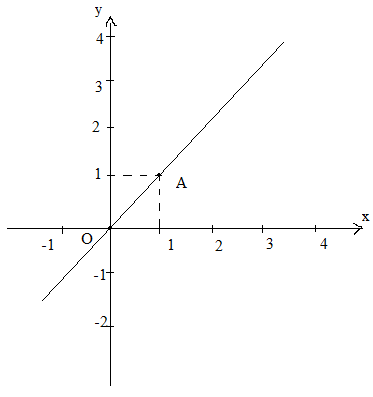
b) Vẽ đồ thị y = 2x.
Đồ thị đi qua O(0;0). Cho x = 1 \( \Rightarrow \) y =2.
Ta có: B(1;2). Vẽ đường thẳng OB ta có đồ thị hàm số.
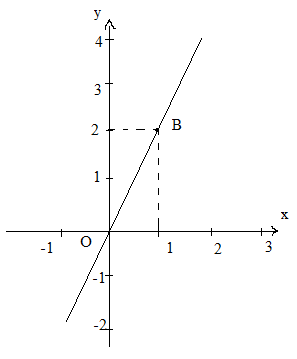
c) Vẽ đồ thị y = -2x.
Advertisements (Quảng cáo)
Đồ thị đi qua O(0;0). Cho x = 1 \( \Rightarrow \) y = -2.
Ta có: C(1;-2). Vẽ đường thẳng OC ta có đồ thị hàm số.
Câu 70: Cho hàm số \(y = 5{{\rm{x}}^2} – 2\). Những điểm nào sau đây thuộc đồ thị của hàm số trên:
\(A\left( {{1 \over 2}; – {3 \over 4}} \right),B\left( {{1 \over 2}; – 1{3 \over 4}} \right),C\left( {2;18} \right)\)
Thay hoành độ điểm A vào công thức hàm số, ta có:
Advertisements (Quảng cáo)
\(y = 5.{\left( {{1 \over 2}} \right)^2} – 2 = {5 \over 4} – 2 = {5 \over 4} – {8 \over 4} = {{ – 3} \over 4} = {y_A}\)
Vậy \({\rm{A}}\left( {{1 \over 2}; – {3 \over 4}} \right)\) thuộc đồ thị hàm số.
Thay hoành độ điểm B vào công thức hàm số, ta có:
\(y = 5.{\left( {{1 \over 2}} \right)^2} – 2 = {5 \over 4} – 2 = {5 \over 4} – {8 \over 4} = {{ – 3} \over 4} \ne {y_B}\)
Vậy điểm B không thuộc đồ thị hàm số
Thay hoành độ điểm C vào công thức hàm số, ta có:
\(y = {5.2^2} – 2 = 5.4 – 2 = 20 – 2 = 18 = {y_C}\)
Vậy C(2;18) thuộc đồ thị hàm số.
Câu 71: Giả sử A và B là hai điểm thuộc đồ thị của hàm số y = 3x + 1.
a) Tung độ của A bằng bao nhiêu nếu hoành độ của nó bằng \({2 \over 3}\)?
b) Hoành độ của B bằng bao nhiêu nếu tung độ của nó bằng –8?
Cho hai điểm A, B thuộc đồ thị hàm số y = 3x + 1
a) Ta có:
\({{\rm{x}}_B} = {2 \over 3} \Rightarrow {y_{A2}} = 3.{2 \over 3} + 1 = 2 + 1 = 3\)
b) Ta có:
\({y_B} = – 8 \Rightarrow {x_B} = {{y – 1} \over 3} = {{ – 8 – 1} \over 3} = {{ – 9} \over 3}\)

