Cho tam giác ABC có \(\widehat B > \widehat C\). Gọi AH là đường vuông góc kẻ từ A đến BC (H thuộc BC) và M là một điểm thuộc đoạn AH. So sánh độ dài BH và CH … trong Kiểm tra 15 phút Toán Chương 3 – Hình học 7. Xem Đề và đáp án đầy đủ phía dưới đây

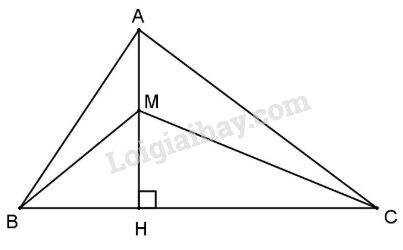
Cho tam giác ABC có \(\widehat B > \widehat C\). Gọi AH là đường vuông góc kẻ từ A đến BC (H thuộc BC) và M là một điểm thuộc đoạn AH.
a) So sánh độ dài BH và CH.
b) So sánh độ dài MB và MC.
c) Chứng minh rằng: \(AH < \dfrac{{AB + AC}}{2}\).
Advertisements (Quảng cáo)

a) \(\widehat B > \widehat C\) (gt) \( \Rightarrow AC > AB\) (quan hệ góc cạnh).
Advertisements (Quảng cáo)
Vì \(AC > AB \Rightarrow HC > HB\)(quan hệ đường xiên hình chiếu).
b) Vì \(HC > HB \Rightarrow MC > MB\) (quan hệ đường xiên hình chiếu).
c) Ta có \(AH < AB\) (đường vuông góc ngắn hơn đường xiên).
Tương tự \(AH < AC\)
\( \Rightarrow 2AH < AB + AC \)
\(\Rightarrow AH < \dfrac{{AB + AC}}{ 2}\).

