
Cho tam giác ABC có \(AB < AC\), AD là phân giác góc A (D thuộc BC). Trên cạnh AC lấy điểm E sao cho \(A{\rm{E}} = AB\).
a) Chứng minh rằng: \(C{\rm{D}} > B{\rm{D}}\);
b) So sánh \(\widehat {ADB}\) và \(\widehat {A{\rm{D}}C}\).

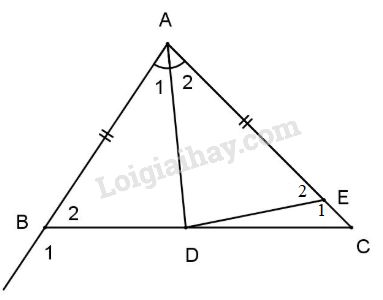
a) Xét \(\Delta A{\rm{D}}B\) và \(\Delta A{\rm{D}}E\) có:
Advertisements (Quảng cáo)
+) AD cạnh chung
+) \({\widehat A_1} = {\widehat A_2}\) (gt)
+) \(AB = A{\rm{E}}\) (gt)
Do đó \(\Delta A{\rm{D}}B = \Delta A{\rm{D}}E\) (c.g.c)
Advertisements (Quảng cáo)
\(\Rightarrow DB = DE\) (cạnh tương ứng) và \({\widehat B_2} = {\widehat E_2}\) (góc tương ứng),
Mà \({\widehat B_1} + {\widehat B_2} = {180^0};{\widehat E_1} + {\widehat E_2} = {180^0}\).
Do đó \({\widehat B_1} = {\widehat E_1}\), mà \({\widehat B_1} > \widehat C\) (vì \({\widehat B_1}\) là góc ngoài của \(\Delta ABC\))
\( \Rightarrow {\widehat E_1} > \widehat C\) (1)
Trong \(\Delta D EC\) có \( {\widehat E_1} > \widehat C\) \( \Rightarrow CD > DE\) mà \(DE = DB\)
\( \Rightarrow C{\rm{D}} > DB\) .
b) \(AB < AC\) (gt) \( \Rightarrow A{\rm{E}} < AC\) (vì \(A{\rm{E}} = AB\))
\( \Rightarrow \widehat {A{\rm{D}}E} < \widehat {A{\rm{D}}C}\)
Mà \(\widehat {A{\rm{D}}E} = \widehat {A{\rm{D}}B}\) (cmt)
\( \Rightarrow \widehat {A{\rm{D}}B} < \widehat {A{\rm{D}}C}\).

