
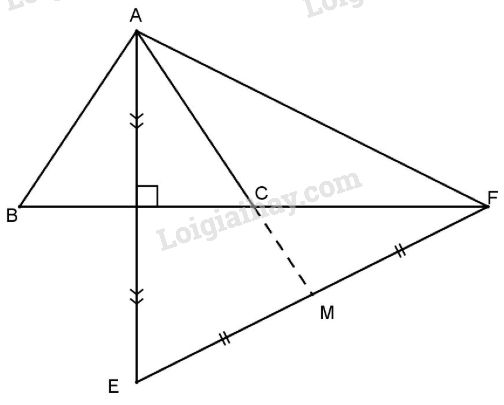
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) trên tia AH lấy E sao cho H là trung điểm của AE. Trên tia đối của tia CB lấy F sao cho \(CF = BC\). Gọi M là trung điểm EB.
Chứng minh rằng: A, C, M thẳng hàng.

Xét hai tam giác vuông AHB và AHC có:
Advertisements (Quảng cáo)
+) AH cạnh chung;
+) \(AB = AC\) (gt).
Advertisements (Quảng cáo)
Do đó \(\Delta AHB = \Delta AHC\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow HB = HC = \dfrac{1 }{ 2}BC,\)
Mà \(CF = BC\) (gt) \( \Rightarrow HC = \dfrac{1 }{ 2}CF\).
Mặt khác H là trung điểm của AE (gt) nên FH là đường trung tuyến của \(\Delta A{\rm{E}}F\), lại có \(HC = \dfrac{1 }{2}CF\) (cmt), do đó C là trọng tâm của \(\Delta A{\rm{E}}F\).
Vì M là trung điểm của EF (gt) nên AM là trung tuyến của \(\Delta A{\rm{E}}F\).
Do đó AM phải đi qua trọng tâm C.
Hay ba điểm A, C, M thẳng hàng.

