
Bài 1: Cho hình vẽ bên, biết a // b và c cắt a, b lần lượt tại A và B biết \(\widehat {{A_1}} = {54^o}.\)
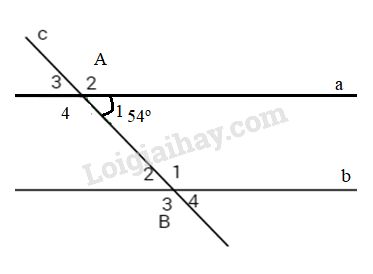
a) Tính \(\widehat {{B_2}}.\)
b) So sánh \(\widehat {{A_4}}\) và \(\widehat {{B_3}}.\)
c) Tính \(\widehat {{A_4}} + \widehat {{B_2}}.\)
Advertisements (Quảng cáo)
Bài 2: Cho tam giác ABC, trên cùng nửa mặt phẳng bờ là đường thẳng AB chứa C, vẽ tia AD sao cho \(\widehat {EAB} = \widehat {ACB} \Rightarrow AE//BC.\) \(\widehat {EAB} = \widehat {ABC}\). Chứng tỏ ba điểm E, A, D thẳng hàng.

Bài 1: a) a // b \( \Rightarrow \widehat {{B_2}} = \widehat {{A_1}} = {54^o}\) (cặp góc so le trong).
Advertisements (Quảng cáo)
b) \(\widehat {{B_3}} = \widehat {{A_4}}\) (cặp góc đồng vị).
c) \(\widehat {{A_4}} + \widehat {{B_2}} = {180^o}\) (cặp góc trong cùng phía bù nhau).
Tương tự \(\widehat {EAB} = \widehat {ACB} \Rightarrow AE//BC.\)
Bài 2:
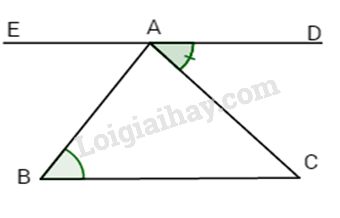
Ta có \(\widehat {DAC} = \widehat {ACB} \Rightarrow AD//BC\) (cặp góc so le trong).
Qua một điểm A có hai đường AD và AE cùng song song với BC thì hai đường thẳng này phải trùng nhau (tiên đề Oclit).
Vậy ba điểm E, A, D thẳng hàng.

