
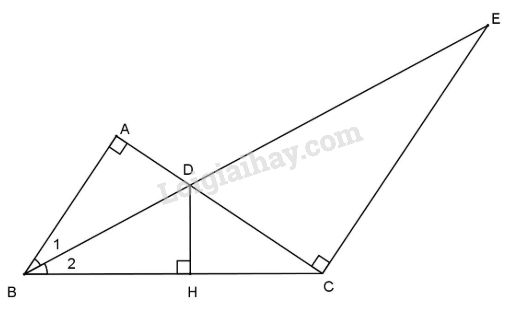
Cho tam giác ABC vuông góc tại A, phân giác góc B cắt AC ở D và cắt đường thẳng vẽ từ C vuông góc với AC tại E.
a) So sánh AB và CE.
b) Kẻ \(DH \bot BC\). So sánh AD và CD.

Advertisements (Quảng cáo)
a) \(AB \bot AC\) (gt);
\(CE \bot AC\) (gt)
\( \Rightarrow AB\) // CE. Do đó \({\widehat B_1} = \widehat E\) (cặp góc so le trong),
Advertisements (Quảng cáo)
Mà \({\widehat B_1} = {\widehat B_2}\) (gt) \( \Rightarrow {\widehat B_2} = \widehat E\)
\( \Rightarrow \Delta BCE\) cân tại C \( \Rightarrow CB = CE.\)
Mặt khác \(\Delta ABC\) vuông tại A ta có \(AB < BC\) (cạnh góc vuông nhỏ hơn cạnh huyền),
Mà \(BC = CE\) (cmt) nên \(AB < CE.\)
b) Dễ thấy \(\Delta BA{\rm{D}} = \Delta BH{\rm{D}}\) (cạnh huyền – góc nhọn)
\( \Rightarrow DH = DA\).
Trong \(\Delta DHC\) vuông tại H ta có \(DH < DC\) (cạnh góc vuông < cạnh huyền) \( \Rightarrow DA < DC.\)

