
Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, qua C kẻ tia Cy vuông góc với AC, gọi I là giao điểm của Bx và Cy.
a) Chứng minh \(\Delta ABI = \Delta ACI.\)
b) Chứng tỏ AI là đường trung trực của đoạn BC.

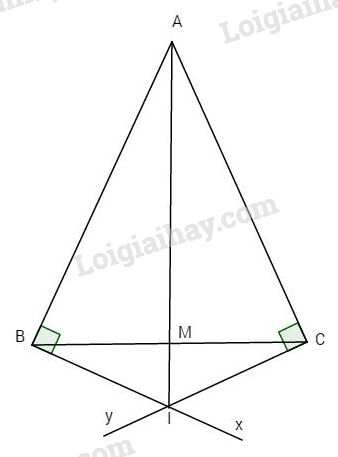
a) Ta có \(Bx \bot AB,\,Cy \bot AC.\)
Xét hai tam giác vuông ABI và ACI có:
Advertisements (Quảng cáo)
+) AI cạnh chung,
+) \(AB = AC\) (giả thiết).
Do đó \(\Delta ABI = \Delta ACI\) (ch.cgv).
b) \(\Delta ABI = \Delta ACI\) (chứng minh trên)
\( \Rightarrow \widehat {BAI} = \widehat {CAI}\) (góc tương ứng).
Advertisements (Quảng cáo)
Gọi M là giao điểm của AI và BC.
Xét \(\Delta AMB\) và \(\Delta AMC\) có:
+) AM cạnh chung;
+) \(\widehat {BAM} = \widehat {CAM}\) (chứng minh trên);
+) \(AB = AC\) (giả thiết).
Do đó \(\Delta AMB = \Delta AMC\) (c.g.c)
\( \Rightarrow MB = MC\,\;(1)\) và \(\widehat {AMB} = \widehat {AMC}\).
Mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\) (kề bù)
\( \Rightarrow \widehat {AMB} = \widehat {AMC} = {90^o}\).
Chứng tỏ \(AM \bot BC\) (2).
Từ (1) và (2) \( \Rightarrow AI\) là đường trung trực của BC.

