
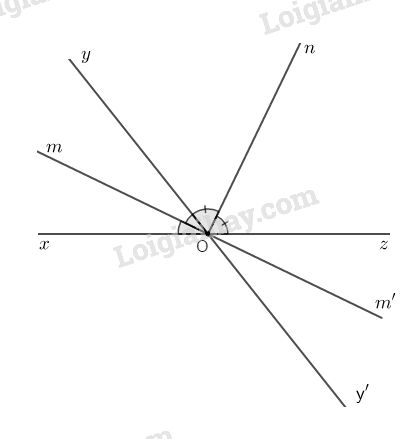
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}.\) Gọi Om, On lần lượt là các tia phân giác của \(\widehat {xOy}\) và \(\widehat {yOz}.\)
a) Tính số đo góc \(\widehat {mOn}.\)
b) Vẽ góc \(\widehat {zOy’}\) là góc đối đỉnh với góc \(\widehat {xOy}\) và Om’ là tia đối của tia Om. Chứng minh Om’ là tia phân giác của góc \(\widehat {y’Oz}\) và On là tia phân giác ảu góc \(\widehat {mOm’}.\)

Advertisements (Quảng cáo)
a) Ta có Om là tia phân giác của \(\widehat {xOy}\) nên
\(\widehat {xOm} = \widehat {yOm} =\dfrac {1 }{2}\widehat {xOy}.\)
Tương tự: \(\widehat {mOm’} + \widehat {nOm’} = {180^o}\)
Advertisements (Quảng cáo)
\(\Rightarrow \widehat {nOm’} = \widehat {mOn} = {90^o},\) \(\widehat {yOn} = \widehat {zOn} = \dfrac{1 }{ 2}\widehat {yOz}\)
Mà \(\widehat {xOy} = \widehat {yOz} = {180^o}\)
\( \Rightarrow \widehat {xOm} = \widehat {yOn} = {90^o}\) hay \(\widehat {mOn} = {90^o}.\)
b) Ta có \(\widehat {zOy’} = \widehat {xOy}\) (đối đỉnh) và Om’ là hai tia đối của tia Om nên \(\widehat {xOm}\)và \(\widehat {zOm’}\), \(\widehat {yOm}\)và \(\widehat {y’Om’}\) là các cặp góc đối đỉnh.
\( \Rightarrow \widehat {zOm’} = \widehat {y’Om’},\) chứng tỏ Om’ là hai phân giác của góc \(\widehat {zOy’}\).
Theo chứng minh trên ta có \(\widehat {mOn} = {90^o}\) mà Om’ và Om là hai tia đối nhau nên \(\widehat {mOn} + \widehat {nOm’} = {180^o}\)
\(\Rightarrow \widehat {nOm’} = \widehat {mOn} = {90^o},\)
Chứng tỏ On là hai tia phân giác của \(\widehat {mOm’}\).

