Cho tam giác ABC có \(AB > AC\), tia phân giác của góc A cắt BC ở D. Trên đoạn thẳng AD lấy điểm E. Chứng minh rằng: \(AB – AC > EB – EC\) trong Đề kiểm tra 15 phút môn Toán Chương 3 – Hình học 7. Xem Đề và đáp án đầy đủ phía dưới đây

Cho tam giác ABC có \(AB > AC\), tia phân giác của góc A cắt BC ở D. Trên đoạn thẳng AD lấy điểm E. Chứng minh rằng: \(AB – AC > EB – EC\).

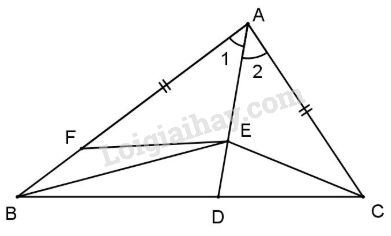
Vì \(AB > AC\) (gt) nên trên AB lấy điểm F sao cho \(AF = AC\).
Advertisements (Quảng cáo)
Khi đó \(\Delta AEF = \Delta A{\rm{E}}C\) (c.g.c)
\( \Rightarrow EF = EC\).
Advertisements (Quảng cáo)
Xét \(\Delta {\rm B}{\rm E}F\), theo bất đẳng thức tam giác
\( \Rightarrow BF > BE – F{\rm{E}}\), mà \(BF = AB – AF\)
\( \Rightarrow AB – AF > EB – F{\rm{E}}\).
Mặt khác \(AF = AC;F{\rm{E}} = EC\).
Do đó \(AB – AC > EB – EC.\)

