
Cho tam giác ABC có \(\widehat A = {80^o}\) và \(\widehat B = {40^o}\). Tia phân giác của góc C cắt AB tại D. Tính số đo \(\widehat {CDA}\) và \(\widehat {CDB}\).

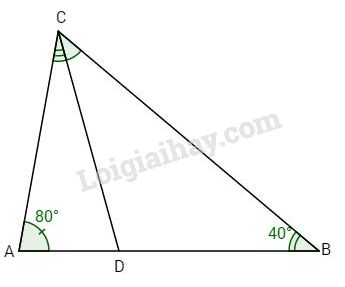
Ta có \(\widehat A + \widehat B + \widehat C = {180^o}\)
Advertisements (Quảng cáo)
\(\Rightarrow \widehat C = {180^o} – \left( {\widehat A + \widehat B} \right)\)
\( \;\;\;\;\;\;\;\;\;= {180^o} – \left( {{{80}^o} + {{40}^o}} \right)=60^o\)
Advertisements (Quảng cáo)
CD là phân giác của góc \(\widehat C\) nên ta có:
\(\widehat {ACD} = \widehat {BCD} =\dfrac {{\widehat {ACB}}}{2} = \dfrac{{{{60}^o}} }{ 2} = {30^o}.\)
Xét ta có \(\widehat A + \widehat {ACD} + \widehat {CDA} = {180^o}\)
\( \Rightarrow \widehat {CDA} = {180^o} – \left( {\widehat A + \widehat {ACD}} \right)\)
\(\eqalign{ & = {180^o} – \left( {{{80}^o} + {{30}^o}} \right) \cr & = {70^o}. \cr} \)
Ta có \(\widehat {CDA} + \widehat {CDB} = {180^o}\)(kề bù) \( \Rightarrow \widehat {CDB} = {180^o} – {70^o} = {110^o}.\)

