
Cho góc \(\widehat {AOB} = {120^o},\) vẽ các tia OC và OD nằm trong góc AOB sao cho \(OC \bot OA\) và \(OD \bot OB\)
a) Tính góc \(\widehat {COD}.\)
b) Gọi Om, On lần lượt là hai tia phân giác của hai góc \(\widehat {AOD}\) và \(\widehat {BOC}\). Chứng minh rằng \(Om \bot On\).

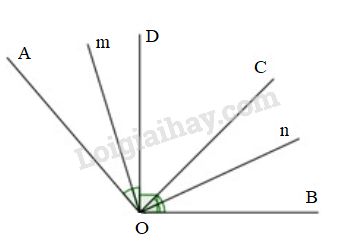
a) Ta có \(OC \bot OA\) nên \(\widehat {OAC} = {90^o}.\)
Advertisements (Quảng cáo)
Tia OC nằm giữa hai tia OA và OB nên
\(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\)
Hay \({90^o} + \widehat {COB} = {120^o} \Rightarrow \widehat {COB} = {30^o}.\)
Advertisements (Quảng cáo)
Chứng minh tương tự ta có \( \Rightarrow \widehat {DOm} + \widehat {DOC} + \widehat {COn}\)\( = {15^o} + {60^o} + {15^0} = {90^o},\) \(\widehat {AOD} = {30^o}.\)
Do đó
\(\widehat {DOC} = \widehat {AOB} – \left( {\widehat {AOD} + \widehat {COB}} \right)\)
\( \;\;\;\;\;\;\;\;\;\;= {120^o} – \left( {{{30}^o} + {{30}^o}} \right)={60^o}.\)
b) Om là tia phân giác của \(\widehat {AOD}\) nên \(\widehat {AOm} = \widehat {DOm} = {{\widehat {AOD}} \over 2} = {15^o}.\)
Tương tự On là phân giác của \(\widehat {BOC}\) nên
\(\widehat {BOn} = \widehat {COn} = {{\widehat {COB}} \over 2} = {15^o}.\)
\( \Rightarrow \widehat {DOm} + \widehat {DOC} + \widehat {COn} \)\(\,= {15^o} + {60^o} + {15^0} = {90^o},\)
Chứng tỏ \(Om \bot On.\)

