
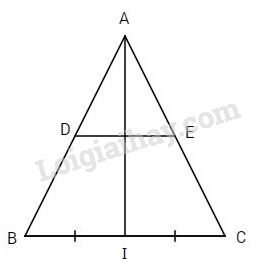
Cho tam giác ABC cân tại A, trên các cạnh AB và AC lấy tương ứng hai điểm D và E sao cho AD = AE.
a) Chứng minh rằng DE // BC.
b) Gọi I là trung điểm của BC. Chứng minh AI là đườngt rung trực của đoạn BC.

a) Ta có AD = AE (giả thiết), nên tam giác ADE cân tại A và \(\widehat A + \widehat {ADE} + \widehat {AED} = {180^o}\)
Advertisements (Quảng cáo)
\(\widehat {ADE} = \widehat {AED} = {{{{180}^o} – \widehat A} \over 2}\) (1)
Tương tự tam giác ABC cân tại A nên
\(\widehat {ABC} = \widehat {ACB} = {{{{180}^o} – \widehat A} \over 2}\)
Từ (1) và (2) \( \Rightarrow \widehat {ADE} = \widehat {ABC}\).
Advertisements (Quảng cáo)
Do đó DE // BC (cặp góc đồng vị bằng nhau).
b) Xét \(\Delta AIB \) và \( \Delta AIC\) có:
+) AI cạnh chung,
+) IB = IC (giả thiết),
+) AB = AC (giả thiết)
\(\Rightarrow \Delta AIB = \Delta AIC\) (c.c.c)
\( \Rightarrow \widehat {AIB} = \widehat {AIC} = {90^o}\) hay \(AI \bot BC.\)
Mặt khác I là trung điểm của BC (giả thiết).
Vậy AI là đường trung trực của đoạn thẳng BC.

