
Cho góc nhọn \(\widehat {xOy}\), lấy A thuộc Ox, B thuộc Oy sao cho OA = OB, kẻ AH vuông góc với Oy và BK vuông góc với Ox.
a) Chứng minh \(\Delta OHK\) cân.
b) Gọi I là giao điểm của AH và BK. Chứng minh OI là tia phân giác của \(\widehat {xOy}\).

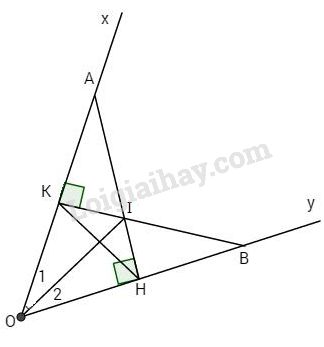
a) Xét hai tam giác vuông OHA và OKB có:
+) \(\widehat O\) chung,
+) \(OA = OB\) (giả thiết)
Advertisements (Quảng cáo)
Vậy \(\Delta OHA = \Delta OKB\) (g.c.g)
\( \Rightarrow OH = OK\) (cạnh tương ứng)
Vậy tam giác OHK cân tại O.
b) Ta có OA = OB (giả thiết),
OK = OH (chứng minh trên)
Advertisements (Quảng cáo)
\( \Rightarrow OA – OK = OB – OH\) hay \(AK = HB.\) (1)
Xét hai tam giác vuông IKA và IHB có AK = HB (chứng minh trên)
Và \(\widehat {KAI} = \widehat {HBI}\) (chứng minh trên)
\( \Rightarrow \Delta IKA = \Delta IHB\) (g.c.g)
Do đó IA = IB (chứng minh trên)
Xét \(\Delta OIA \) và \( \Delta OIB\) có:
+) IO chung
+) OA= OB (giả thiết)
+) IA = IB (chứng minh trên)
\( \Rightarrow \Delta OIA = \Delta OIB\) (c.c.c)
\( \Rightarrow \widehat {AOI} = \widehat {BOI}\) (2 góc tương ứng)
Hay OI là tia phân giác của \(\widehat {xOy}\).

