Bài 1.29: Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau:
a) \(y = {{2x – 1} \over {x + 2}}\);
b) \(y = {{3 – 2x} \over {3x + 1}}\)
c) \(y = {5 \over {2 – 3x}}\)
d) \(y = {{ – 4} \over {x + 1}}\)
a) \(y = {{2x – 1} \over {x + 2}}\)
Ta có: \(\mathop {\lim }\limits_{x \to – {2^ + }} {{2x – 1} \over {x + 2}} = – \infty ,\mathop {\lim }\limits_{x \to – {2^ – }} {{2x – 1} \over {x + 2}} = + \infty \) nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì \(\mathop {\lim }\limits_{x \to \pm \infty } {{2x – 1} \over {x + 2}} = \mathop {\lim }\limits_{x \to \pm \infty } {{2 – {1 \over x}} \over {1 + {2 \over x}}} = 2\) nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
b) Từ \(\mathop {\lim }\limits_{x \to {{( – {1 \over 3})}^ + }} {{3 – 2x} \over {3x + 1}} = + \infty ;\mathop {\lim }\limits_{x \to {{( – {1 \over 3})}^ – }} {{3 – 2x} \over {3x + 1}} = – \infty \) , ta có \(x = – {1 \over 3}\) là tiệm cận đứng
Vì \(\mathop {\lim }\limits_{x \to \pm \infty } {{3 – 2x} \over {3x + 1}} = \mathop {\lim }\limits_{x \to \pm \infty } {{{3 \over x} – 2} \over {3 + {1 \over x}}} = – {2 \over 3}\) nên đường thẳng \(y = – {2 \over 3}\) là tiệm cận ngang.
c) Vì \(\mathop {\lim }\limits_{x \to {{({2 \over 3})}^ + }} {5 \over {2 – 3x}} = – \infty ;\mathop {\lim }\limits_{x \to {{({2 \over 3})}^ – }} {5 \over {2 – 3x}} = + \infty \) nên \(x = {2 \over 3}\) là tiệm cận đứng,
Do \(\mathop {\lim }\limits_{x \to \pm \infty } {5 \over {2 – 3x}} = 0\) nên y = 0 là tiệm cận ngang.
d) Do \(\mathop {\lim }\limits_{x \to – {1^ + }} {{ – 4} \over {x + 1}} = – \infty ;\mathop {\lim }\limits_{x \to – {1^ – }} {{ – 4} \over {x + 1}} = + \infty \) nên x = -1 là tiệm cận đứng.
Vì \(\mathop {\lim }\limits_{x \to \pm \infty } {{ – 4} \over {x + 1}} = 0\) nên y = 0 là tiệm cận ngang.
Bài 1.30: Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau:
a) \(y = {{{x^2} – 12x + 27} \over {{x^2} – 4x + 5}}\)
Advertisements (Quảng cáo)
b) \(y = {{{x^2} – x – 2} \over {{{(x – 1)}^2}}}\)
c) \(y = {{{x^2} + 3x} \over {{x^2} – 4}}\)
d) \(y = {{2 – x} \over {{x^2} – 4x + 3}}\)
e) \(y = {{3x + \sqrt {{x^2} + 1} } \over {2 + \sqrt {3{x^2} + 2} }}\)
f) \(y = {{5x – 1 – \sqrt {{x^2} – 2} } \over {x – 4}}\)
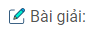
a) Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } {{{x^2} – 12x + 27} \over {{x^2} – 4x + 5}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 – {{12} \over x} + {{27} \over {{x^2}}}} \over {1 – {4 \over x} + {5 \over {{x^2}}}}} = 1\) nên y = 1 là tiệm cận ngang.
b) Vì \(\mathop {\lim }\limits_{x \to {1^ \pm }} {{{x^2} – x – 2} \over {{{(x – 1)}^2}}} = – \infty \) nên x = 1 là tiệm cận đứng.
Từ \(\mathop {\lim }\limits_{x \to \pm \infty } {{{x^2} – x – 2} \over {{{(x – 1)}^2}}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 – {1 \over x} – {2 \over {{x^2}}}} \over {{{(1 – {1 \over x})}^2}}} = 1\) suy ra y = 1 là tiệm cận ngang.
c) Vì \(\mathop {\lim }\limits_{x \to {2^ + }} {{{x^2} + 3x} \over {{x^2} – 4}} = \mathop {\lim }\limits_{x \to {2^ + }} {{{x^2} + 3x} \over {(x – 2)(x + 2)}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {2^ – }} {{{x^2} + 3x} \over {(x – 2)(x + 2)}} = – \infty \) nên x = 2 là một tiệm cận đứng.
Do \(\mathop {\lim }\limits_{x \to – {2^ + }} {{{x^2} + 3x} \over {{x^2} – 4}} = + \infty \) và \(\mathop {\lim }\limits_{x \to – {2^ – }} {{{x^2} + 3x} \over {(x – 2)(x + 2)}} = – \infty \) nên x = -2 là tiệm cận đứng thứ hai.
Advertisements (Quảng cáo)
Ta lại có \(\mathop {\lim }\limits_{x \to \pm \infty } {{{x^2} + 3x} \over {{x^2} – 4}} = \mathop {\lim }\limits_{x \to \pm \infty } {{1 + {3 \over x}} \over {1 – {4 \over {{x^2}}}}} = 1\) nên y = 1 là tiệm cận ngang.
d) Do \(\mathop {\lim }\limits_{x \to {1^ \pm }} {{2 – x} \over {{x^2} – 4x + 3}} = \mathop {\lim }\limits_{x \to {1^ \pm }} {{2 – x} \over {(x – 1)(x – 3)}} = \mp \infty\) nên x = 1 là tiệm cận đứng.
Mặt khác, \(\mathop {\lim }\limits_{x \to {3^ \pm }} {{2 – x} \over {{x^2} – 4x + 3}} = \mp \infty \) nên x = 3 cũng là tiệm cận đứng
Vì \(\mathop {\lim }\limits_{x \to \pm \infty } {{2 – x} \over {{x^2} – 4x + 3}} = 0\) nên y = 0 là tiệm cận ngang.
e) TXĐ: R
Từ \(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{3 + \sqrt {1 + {1 \over {{x^2}}}} } \over {{2 \over x} + \sqrt {3 + {2 \over {{x^2}}}} }} = {4 \over {\sqrt 3 }} = {{4\sqrt 3 } \over 3} \cr
& \mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {{3 – \sqrt {1 + {1 \over {{x^2}}}} } \over {{2 \over x} – \sqrt {3 + {2 \over {{x^2}}}} }} = – {2 \over {\sqrt 3 }} = – {{2\sqrt 3 } \over 3} \cr} \)
Suy ra đồ thị hàm số có các tiệm cận ngang:
\(y = {{4\sqrt 3 } \over 3}\) khi \(x \to + \infty \)
\(y = – {{2\sqrt 3 } \over 3}\) khi \(x \to – \infty \)
Đồ thị hàm số không có tiệm cận đứng.
f) TXĐ: \(D = ( – \infty ; – \sqrt 2 ) \cup (\sqrt 2 ;4) \cup (4; + \infty )\)
Do \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{5 – {1 \over x} – \sqrt {1 – {2 \over {{x^2}}}} } \over {1 – {4 \over x}}} = 4\)
\(\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {{5 – {1 \over x} + \sqrt {1 – {2 \over {{x^2}}}} } \over {1 – {4 \over x}}} = 6\)
Cho nên đồ thị hàm số có hai tiệm cận ngang
y = 4 khi \(x \to + \infty \)
y = 6 khi \(x \to – \infty \)
Vì \(\mathop {\lim }\limits_{x \to {4^ \pm }} y = \mathop {\lim }\limits_{x \to {4^ \pm }} {{5x – 1 – \sqrt {{x^2} – 2} } \over {x – 4}} = \pm \infty \)
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.
Bài 1.31: a) Cho hàm số \(y = {{3 – x} \over {x + 1}}\) có đồ thị (H)
 Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.
b) Lấy đối xứng (H’) qua gốc (O), ta được hình (H’’). Viết phương trình của (H’’).
a) Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
\(\eqalign{
& y = f(x) = {{3 – x} \over {x + 1}} + 3 = {{3 – x + 3x + 3} \over {x + 1}} = {{2x + 6} \over {x + 1}} \cr
& y = g(x) = {{2(x – 3) + 6} \over {x – 3 + 1}} = {{2x} \over {x – 2}} \cr} \)
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là:
\(y = h(x) = – {{2( – x)} \over {( – x) – 2}} = – {{ – 2x} \over { – 2 – x}} = – {{2x} \over {x + 2}}\).

