
1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tính chiều cao h của hình chóp S. ABCD, biết thể tích khối chóp S.ABCD là a3.
A. h = a B. h = 2a
C. h = 3a D. h = 4a
2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC.
\(A.V = \,\,\dfrac{{{a^3}}}{2}\) \(B.\,\,V = {a^3}\)
\(C.\,\,V = \dfrac{{3{a^3}}}{2}\) \(D.\,\,V = \dfrac{{{a^3}}}{2}\)
3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE = 2EC. Tính thể tích V của khối tứ diện SEBD.
\(A.\,\,V = \dfrac{1}{3}\) \(B.\,\,V = \dfrac{1}{6}\)
\(C.\,\,V = \dfrac{1}{{12}}\) \(D.\,\,V = \dfrac{2}{3}\)
4. Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh \(AB = a,AD = a\sqrt 2 ,SA \bot (ABCD)\), góc giữa SC và đáy bằng \({60^o}\). Thể tích hình chóp S.ABCD bằng:
\(A.\,\,3\sqrt 2 {a^3}\) \(B.\,\,3{a^3}\)
\(C.\,\,\sqrt 6 {a^3}\) \(D.\,\,\sqrt 2 {a^3}\)
5. Hình chóp S.ABC có đáy là tam giác vuông tại A, cạnh AB = a, BC = 2a, chiều cao \(SA = a\sqrt 6 \). Thể tích của khối chóp là:
\(A.\,\,V = \dfrac{{{a^3}\sqrt 2 }}{2}\) \(B.\,\,V = \dfrac{{{a^3}\sqrt 6 }}{3}\)
\(C.\,\,V = \dfrac{{{a^3} }}{2}\) \(D.\,\,V = 2{a^3}\sqrt 6 \)
6. Cho hình chóp S. ABCD có đáy là hình chữ nhật với Ab = a, AD = 2a, SA vuông góc với mặt đáy và \(SA = a\sqrt 3 \). Thể tích khối chóp S.ABC bằng:
\(A.\,\,V = \dfrac{{2{a^3}\sqrt 3 }}{3}\) \(B.\,\,V = \dfrac{{{a^3}\sqrt 3 }}{3}\)
\(C.\,\,V = {a^3}\sqrt 3 \) \(D.\,\,V = 2{a^3}\sqrt 3 \)
7. Cho hình chóp tứ giác đều S.ABCD có canhj đáy bẳng a và mặt bên tạo với đáy một góc 45o. Thể tích V khối chóp S.ABCD là:
\(A.\,\,V = \dfrac{{{a^3}}}{2}\) \(B.\,\,V = \dfrac{{{a^3}}}{9}\)
\(C.\,\,V = \dfrac{{{a^3}}}{6}\) \(D.\,\,V = \dfrac{{{a^3}}}{{24}}\)

|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
C |
B |
A |
D |
A |
B |
C |
1. Ta có: \({V_{S.ABCD}} = \dfrac{1}{3}.h.{S_{ABCD}}\)
Advertisements (Quảng cáo)
Khi đó ta có: \(h = \dfrac{{3{V_{S.ABCD}}}}{{{S_{ABCD}}}} = \dfrac{{3{a^3}}}{{{a^2}}} = 3a.\)
Chọn đáp án C.
2. Tam giác SAB nằm trong mặt phẳng vuông góc với đáy.
Gọi H là trung điểm của AB
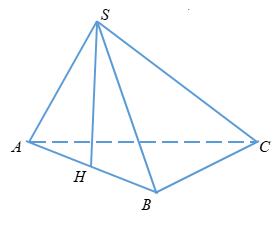
\( \Rightarrow SH \bot AB\) hay \(SH \bot \left( {ABC} \right)\)
Ta có: \(SA = SB = AB = 2a\)
\(\Rightarrow SH = \sqrt {4{a^2} – {a^2}} = a\sqrt 3 \)
+ \({S_{ABC}} = \dfrac{1}{2}a\sqrt 3 .2a = {a^2}\sqrt 3 \)
Khi đó \({V_{S.ABC}} = \dfrac{1}{3}.a\sqrt 3 .{a^2}\sqrt 3 = {a^3}\)
Chọn đáp án B.
3.
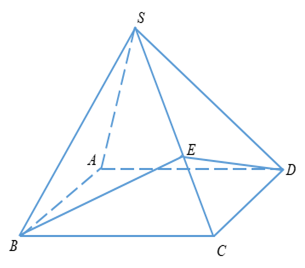
Ta có:\(\dfrac{{{V_{S.BED}}}}{{{V_{S.BCD}}}} = \dfrac{{SE}}{{SC}} = \dfrac{2}{3}\)
\(\dfrac{{{V_{S.BCD}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{2}\)
Advertisements (Quảng cáo)
\( \Rightarrow {V_{S.BED}} = \dfrac{2}{3}.\dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{3}\)
Chọn đáp án A.
4.
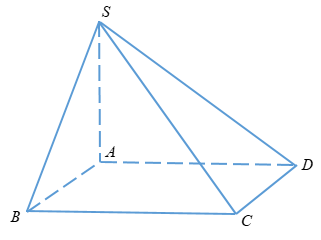
Xét tam giác SAC có
\(\tan {60^ \circ } = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{B^2} + B{C^2}} }}\)\(\, = \dfrac{{SA}}{{a\sqrt 3 }}\)
\(\Rightarrow SA = 3a\)
Khi đó:
\({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} \)\(\,= \dfrac{1}{3}.3a.a.a\sqrt 2 = {a^3}\sqrt 2 \)
Chọn đáp án D.
5.
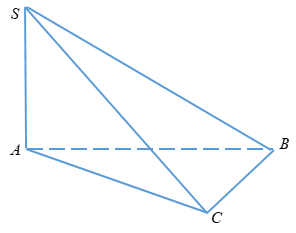
Áp dụng định lý Py – ta- go ta có:
\(AC = \sqrt {B{C^2} – A{B^2}} \)
\(\;\;\;\;\;\; = \sqrt {4{a^2} – {a^2}} = a\sqrt 3 \)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}a.a\sqrt 3 \)\(\, = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Khi đó:
\({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} \)\(\,= \dfrac{1}{3}a\sqrt 6 .\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 2 }}{2}\)
Chọn đáp án A.
6.
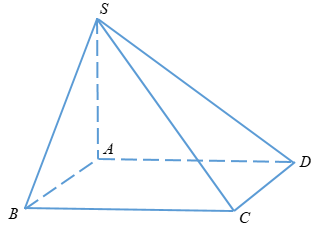
Ta có:
\({S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a.2a = {a^2}\)
Khi đó
\({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.a\sqrt 3 .{a^2} \)\(\,= \dfrac{{{a^3}\sqrt 3 }}{3}\)
Chọn đáp án B.
7. Ta có:
\(\tan {45^0} = \dfrac{{SO}}{{OE}} = \dfrac{{SO}}{{\dfrac{a}{2}}} \Rightarrow SO = \dfrac{a}{2}\)
Khi đó:
\({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{a}{2}.{a^2}\)\(\, = \dfrac{{{a^3}}}{6}\)
Chọn đáp án C.

