
1. Hình chóp S.ABC có đáy là tam giác vuông tại A, cạnh AB = a, BC = 2a, chiều cao \(SA = a\sqrt 6 \). Thể tích của khối chóp là:
\(A.\,\,V = \dfrac{{{a^3}\sqrt 2 }}{2}\) \(B.\,\,V = \dfrac{{{a^3}\sqrt 6 }}{3}\)
\(C.\,\,V = \dfrac{{{a^3}\sqrt 2 }}{2}\) \(D.\,\,V = 2{a^3}\sqrt 6 \)
2. Cho hình chóp S. ABCD có đáy ABCD là hình chứ nhật có AB = a, AC = 5a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với đáy, cạnh bên SB tạo với đáy một góc bằng 60o. Tính theo a thể tích của khối chóp S.ABCD.
\(A.\,\,2\sqrt 2 {a^3}\) \(B.\,4\sqrt 2 {a^3}\)
\(C.\,\,6\sqrt 2 {a^3}\) \(D.\,\,2{a^3}\)
3. Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh 2a. Cạnh bên SC vuông góc với mặt phẳng đáy và SC = a. Thể tích V của khối chóp S.ABC là:
\(A.\,\,V = 2{a^3}\sqrt 3 \) \(B.\,\,V = \dfrac{{{a^3}\sqrt 3 }}{4}\)
\(C.\,\,V = \dfrac{{{a^3}\sqrt 3 }}{3}\) \(D.\,\,V = {a^3}\sqrt 3 \)
4. Hình hộp đứng ABCD.A’B’C’D’ có đáy là một hình thôi có góc nhọn bằng \(\alpha \), cạnh a. Diện tích xung quanh của hình hộp đó bằng S. Tính thể tích của khối hộp ABCD.A’B’C’D’
\(A.\dfrac{1}{4}a.S.\sin \alpha \) \(B.\,\,\dfrac{1}{2}a.S.\sin \alpha \)
\(C.\,\,\dfrac{1}{8}a.S.\sin \alpha \) \(D.\,\,\dfrac{1}{6}a.S.\sin \alpha \)
5. Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, \(SA = SB = SC = SD = a\sqrt 2 \). Tính thể tích khối chóp S.ABCD.
\(A.\,\dfrac{{{a^3}\sqrt 3 }}{3}\) \(B.\,\dfrac{{{a^3}\sqrt 6 }}{9}\) \(C.\,\dfrac{{{a^3}\sqrt 6 }}{6}\) \(D.\,\dfrac{{{a^3}\sqrt 6 }}{{12}}\)
6. Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi mặt phẳng (SBC) và mặt phẳng (ABC) bằng 30o. Thể tích của khối chóp S.ABC là:
\(A.\,\,\dfrac{{{a^3}\sqrt 3 }}{8}\) \(B.\,\,\dfrac{{{a^3}\sqrt 3 }}{{24}}\) \(C.\,\,\dfrac{{{a^3}}}{4}\) \(D.\,\,\dfrac{{{a^3}}}{{12}}\)
7. Hình đa diện nào sau đây có tâm đối xứng?
A. Hình tứ diện đều
B. Hình chóp tứ giác đều
C. Hình lăng trụ tam giác
D. Hình hộp

|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
C |
A |
C |
A |
C |
B |
D |
1.
Advertisements (Quảng cáo)
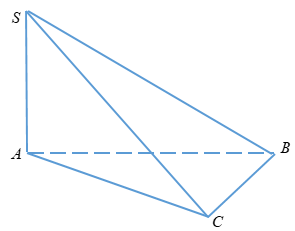
Áp dụng định lý Py – ta- go ta có:
\(AC = \sqrt {B{C^2} – A{B^2}} \)
\(\;\;\;\;\;\;\;= \sqrt {4{a^2} – {a^2}} = a\sqrt 3 \)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}a.a\sqrt 3 \)\(\, = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Khi đó:
\({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}a\sqrt 6 .\dfrac{{{a^2}\sqrt 3 }}{2} \)\(\,= \dfrac{{{a^3}\sqrt 2 }}{2}\)
Chọn đáp án C.
2..
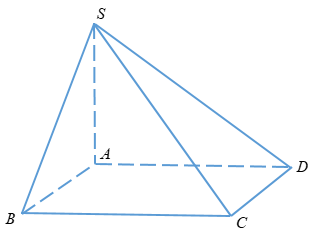
Theo giả thiết ta có mặt bên (SAB) và (SAD) cùng vuông góc với đáy.
\( \Rightarrow SA \bot \left( {ABCD} \right)\)
+ Mà \(\tan {60^0} = \dfrac{{SA}}{{AB}} = \dfrac{{SA}}{a} \Rightarrow SA = a\sqrt 3 \)
+ \(BC = \sqrt {A{C^2} – A{B^2}} \)\(\,= \sqrt {25a{}^2 – {a^2}} = 2a\sqrt 6 \)
Khi đó ta có:
Advertisements (Quảng cáo)
\({V_{S.ABCD}} = \dfrac{1}{3}.SA.{S_{ABCD}} \)\(\,= \dfrac{1}{3}.a\sqrt 3 .2a\sqrt 6 .a = 2{a^3}\sqrt 2 \)
Chọn đáp án A.
3..
Ta có: \({S_{ABC}} = \dfrac{1}{2}.a\sqrt 3 .2a = {a^2}\sqrt 3 \)
Khi đó \({V_{S.ABC}} = \dfrac{1}{3}.SC.{S_{ABC}} \)\(\,= \dfrac{1}{3}.{a^2}\sqrt 3 .a = \dfrac{{{a^3}\sqrt 3 }}{3}\)
Chọn đáp án C.
4..
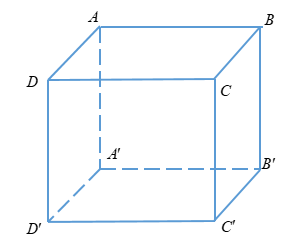
Ta có:
\({S_{xq}} = 2\left( {DD’.D’A’ + DD’.D’C’} \right)\)\(\, = 2DD’\left( {2a} \right) = S\)
\( \Rightarrow DD’ = \dfrac{S}{{4a}}\)
Diện tích đáy bằng:
\({S_d} = 2.\dfrac{1}{2}a.a.\sin \alpha = {a^2}\sin \alpha \)
Khi đó \({V_{ABCD.A’B’C’D’}} = DD’.{S_d} \)\(\,= \dfrac{S}{{4a}}.{a^2}\sin \alpha = \dfrac{1}{4}.Sa\sin \alpha \)
Chọn đáp án A.
5..
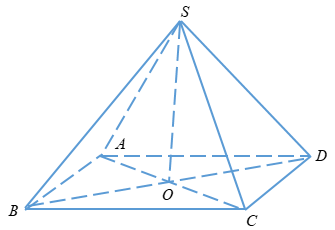
Ta có:
\(OA = OB = OC = OD = \dfrac{{AC}}{2} \)\(\,= \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow SO = \sqrt {S{A^2} – OA{}^2} \)\(\, = \sqrt {2{a^2} – \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 6 }}{2}\)
Khi đó:
\(V = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{2}.{a^2}\)\(\, = \dfrac{{{a^3}\sqrt 6 }}{6}\)
Chọn đáp án C.
6..
Gọi H là trung điểm của BC.
Ta có: \(AH = \sqrt {A{C^2} – H{C^2}} = \sqrt {{a^2} – \dfrac{{{a^2}}}{4}} \)\(\,= \dfrac{{a\sqrt 3 }}{2}\)
+ \(\tan {30^0} = \dfrac{{SA}}{{AH}}\)
\(\Rightarrow SA = \dfrac{{\sqrt 3 }}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{a}{2}\)
Vậy\(V = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.a\)\(\, = \dfrac{{{a^3}\sqrt 3 }}{{24}}\)
Chọn đáp án B
7.. Hình hộp là đa diện có tâm đối xứng.
Chọn đáp án D.

