Bài trắc nghiệm khách quan chương II
Trong mỗi bài tập dưới dây, hãy chọn một phương án cho để được khẳng định đúng.
Bài 98: Giá trị biểu thức \({\log _2}36 – {\log _2}144\) bằng
(A) – 4 ; (B) 4 ;
(C) – 2 ; (D) 2.
Giải: \({\log _2}36 – {\log _2}144 = {\log _2}{{36} \over {144}} = {\log _2}{1 \over 4}\)
\(= {\log _2}{2^{ – 2}} = – 2\)
Chọn (C).
Bài 99: Biết \({\log _6}\sqrt a = 2\) thì \({\log _6}a\) bằng:
(A) 36 ; (B) 108 ;
(C) 6 ; (D) 4.
Giải: \({\log _6}\sqrt a = 2 \Leftrightarrow {\log _6}{a^{{1 \over 2}}} = 2 \Leftrightarrow {\log _6}a = 4\)
Chọn (D)
Bài 100: Tập các số x thỏa mãn \({\log _{0,4}}\left( {x – 4} \right) + 1 \ge 0\) là:
\(\left( A \right)\,\left( {4; + \infty } \right)\) \(\left( B \right)\,\left( {4;6,5} \right)\)
\(\left( C \right)\,\left( { – \infty ;6,5} \right)\) \(\left( D \right)\,\left[ {6,5; + \infty } \right)\)
Giải: \(\eqalign{
& {\log _{0,4}}\left( {x – 4} \right) + 1 \ge 0 \Leftrightarrow {\log _{0,4}}\left( {x – 4} \right) \ge – 1 \cr
& \Leftrightarrow 0 < x – 4 \le {\left( {0,4} \right)^{ – 1}} = {5 \over 2} \Leftrightarrow 4 < x \le {{13} \over 2} \cr} \)
Vậy \(S = \left( {4;6,5} \right]\). Chọn (B).
Bài 101: Tập các số x thỏa mãn \({\left( {{2 \over 3}} \right)^{4x}} \le {\left( {{3 \over 2}} \right)^{2 – x}}\) là:
\(\left( A \right)\left( { – \infty ;{2 \over 3}} \right]\) \(\left( B \right)\,\left[ { – {2 \over 3}; + \infty } \right)\)
\(\left( C \right)\,\left( { – \infty ;{2 \over 5}} \right]\) \(\left( D \right)\,\left[ {{2 \over 5}; + \infty } \right)\)
Giải: \(\eqalign{
& {\left( {{2 \over 3}} \right)^{4x}} \le {\left( {{3 \over 2}} \right)^{2 – x}} \Leftrightarrow {\left( {{3 \over 2}} \right)^{ – 4x}} \le {\left( {{3 \over 2}} \right)^{2 – x}} \cr
& \Leftrightarrow – 4x \le 2 – x \Leftrightarrow x \ge – {2 \over 3} \cr} \)
Vậy \(S = \left[ { – {2 \over 3}; + \infty } \right)\). Chọn (B).
Advertisements (Quảng cáo)
Bài 102: Giá trị biểu thức \(3{\log _{0,1}}{10^{2,4}}\) bằng:
(A) 0,8; (B) 7,2;
(C) – 7,2; (D) 72.
Giải: \(3{\log _{0,1}}{10^{2,4}} = 3.2,4{\log _{0,1}}10 = – 7,2\). Chọn (C)
Bài 103: Giá trị biểu thức \(0,5{\log _2}25 + {\log _2}\left( {1,6} \right)\) bằng:
(A) 1; (B) 2;
(C) 3; (D) 5.
Giải: \(\left( {0,5} \right){\log _2}25 + {\log _2}\left( {1,6} \right) = {\log _2}\left( {5.1,6} \right) = {\log _2}8 = 3\)
Chọn (C)
Bài 104: Giá trị biểu thức \({{lo{g_2}240} \over {{{\log }_{3,75}}2}} – {{{{\log }_2}15} \over {{{\log }_{60}}2}} + {\log _2}1\) bằng:
(A) 4; (B) 3;
(C) 1; (D) – 8.
Giải: \(\eqalign{
& {{lo{g_2}240} \over {{{\log }_{3,75}}2}} – {{{{\log }_2}15} \over {{{\log }_{60}}2}} + {\log _2}1\cr& = {lo{g_2}240}.{\log _2}3,75 – {\log _2}15.{\log _2}\left( {15.4} \right) \cr
& = \left( {{{\log }_2}15 + 4} \right){\log _2}{{15} \over 4} – {\log _2}15\left( {{{\log }_2}15 + 2} \right) \cr
& = \left( {{{\log }_2}15 + 4} \right)\left( {{{\log }_2}15 – 2} \right) – {\log _2}15\left( {{{\log }_2}15 + 2} \right) \cr&= – 8 \cr} \)
Chọn (D).
Advertisements (Quảng cáo)
Bài 105: Tập các số x thỏa mãn \({\left( {{3 \over 5}} \right)^{2x – 1}} \le {\left( {{3 \over 5}} \right)^{2 – x}}\) là:
\(\left( A \right)\,\left[ {3; + \infty } \right)\) \(\left( B \right)\,\left( { – \infty ;1} \right]\)
\(\left( C \right)\,\left[ {1; + \infty } \right)\) \(\left( D \right)\,\,\left( { – \infty ; + \infty } \right)\)
Giải: \(2x-1\ge2-x\Leftrightarrow 3x\ge 3\Leftrightarrow x\ge1\)
Vậy \(S = \left[ {1; + \infty } \right)\). Chọn (C).
Bài 106: Đối với hàm số \(f\left( x \right) = {e^{\cos 2x}}\), ta có:
\(\eqalign{
& \left( A \right)\,f’\left( {{\pi \over 6}} \right) = {e^{{{\sqrt 3 } \over 2}}}; \cr
& \left( C \right)\,f’\left( {{\pi \over 6}} \right) = \sqrt {3e} \cr} \)
\(\eqalign{
& \left( B \right)\,f’\left( {{\pi \over 6}} \right) – {e^{{{\sqrt 3 } \over 2}}}; \cr
& \left( D \right)\,f’\left( {{\pi \over 6}} \right) = – \sqrt {3e} \cr} \)
Giải : \(f’\left( x \right) = – 2\sin 2x{e^{\cos 2x}};\,f\left( {{\pi \over 6}} \right)\)
\(= – 2\sin {\pi \over 3}.{e^{\cos {\pi \over 3}}} = – \sqrt 3 .{e^{{1 \over 2}}} = – \sqrt {3e} \)
Chọn (D).
Bài 107: Đối với hàm số \(y = \ln {1 \over {x + 1}}\), ta có:
\(\eqalign{
& \left( A \right)\,xy’ + 1 = {e^y}; \cr
& \left( C \right)\,xy’ – 1 = {e^y}; \cr} \)
\(\eqalign{
& \left( B \right)\,xy’ + 1 = – {e^y}; \cr
& \left( D \right)\,xy’ – 1 = – {e^y}. \cr} \)
Giải : \(\eqalign{
& y = – \ln \left( {x + 1} \right) \Rightarrow y’ = – {1 \over {x + 1}} \cr
& \Rightarrow xy’ + 1 = x.{{ – 1} \over {x + 1}} + 1 = {{ – x} \over {x + 1}} + 1 \cr&= {1 \over {x + 1}} = {e^y} \cr} \)
Chọn (A).
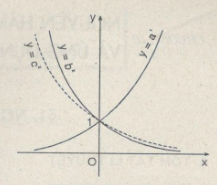
Bài 108: Trên hình bên, đồ thị của ba hàm số: \(y = {a^x};\,y = {b^x};\,y = {c^x}\) (a, b và c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c.
\(\eqalign{
& \left( A \right)\,a > b > c; \cr
& \left( C \right)\,b > a > c; \cr} \)
\(\eqalign{
& \left( B \right)\,a > c > b; \cr
& \left( D \right)\,b > c > a. \cr} \)
Giải
Với x > 0 ta có \({a^x} > {c^x} > {b^x}\) do đó . Chọn (B).
Bài 109: Trên hình bên, đồ thị của ba hàm số:
\(y = {\log _a}x,\,{\log _b}x,\,{\log _c}x\) (a,b và c là ba số dương khác 1 cho trước) được vẽ trong cũng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của logarit, hãy so sánh ba số a,b,c:
\(\eqalign{
& \left( A \right)\,a > b > c; \cr
& \left( C \right)\,b > a > c; \cr} \)
\(\eqalign{
& \left( B \right)\,c > a > b; \cr
& \left( C \right)\,c > b > a. \cr} \)
Giải: Dựa vào tính chất đơn điệu của hàm số ta có: \(a > 1,\,b > 1,\,c > 1\)
Với x > 1 ta có \({\log _a}x > {\log _b}x > 0 \Rightarrow {\log _x}a < {\log _a}b \Rightarrow a < b\)
Vậy \(c < a < b\). Chọn (C).
Bài 110: Phương trình \({\log _2}4x – {\log _{{x \over 2}}}2 = 3\) có bao nhiêu nghiệm?
(A) 1 nghiệm (B) 2 nghiệm
(C) 3 nghiệm (D) 4 nghiệm.
Giải: Điều kiện: \(x > 0,\,x \ne 2\)
\(\eqalign{
& {\log _2}4x – {\log _{{x \over 2}}}2 = 3 \Leftrightarrow 2 + {\log _2}x – {1 \over {{{\log }_2}{x \over 2}}} = 3 \cr
& \Leftrightarrow {\log _2}x – {1 \over {{{\log }_2}x – 1}} = 1 \cr&\Leftrightarrow \log _2^2x – {\log _2}x – 1 = {\log _2}x – 1 \cr
& \Leftrightarrow \log _2^2x – 2{\log _2}x = 0 \cr
& \Leftrightarrow \left[ \matrix{
{\log _2}x = 0 \hfill \cr
{\log _2}x = 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = 4 \hfill \cr} \right. \cr} \)
Phương trinh có 2 nghiệm. Chọn (B).

