Bài 2.18: Hãy so sánh mỗi số sau với 1.
a) \({(0,1)^{\sqrt 2 }}\)
b) \({(3,5)^{0,1}}\)
c) \({\pi ^{ – 2,7}}\)
d) \({(\frac{{\sqrt 5 }}{5})^{ – 1,2}}\)
a) \({(0,1)^{\sqrt 2 }} < 1\)
b) \({(3,5)^{0,1}} > 1\)
c) \({\pi ^{ – 2,7}} < 1\)
d) \({(\frac{{\sqrt 5 }}{5})^{ – 1,2}} > 1\).
Bài 2.19: Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau:
a) \(y = {2^x}\) và y = 8
b) \(y = {3^x}\) và \(y = \frac{1}{3}\)
c) \(y = {(\frac{1}{4})^x}\) và \(y = \frac{1}{{16}}\)
d) \(y = {(\frac{1}{3})^x}\) và y = 9
Advertisements (Quảng cáo)
a) (3; 8)
b) \(( – 1;\frac{1}{3})\)
c) \((2;\frac{1}{{16}})\)
d) (-2; 9).
Bài 2.20: Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau:
a) (1,7)3 và 1
b) (0,3)2 và 1.
c) (3,2)1,5 và (3,2)1,6
d) (0,2)-3 và (0,2)-2
Advertisements (Quảng cáo)
e) \({(\frac{1}{5})^{\sqrt 2 }}\) và \({(\frac{1}{5})^{1,4}}\)
g) \({6^\pi }\) và 63,14
a) (1,7)3 > 1 ;
b) (0,3)2 < 1 ;
c) (3,2)1,5 < (3,2)1,6
d) (0,2)– 3 > (0,2)– 2
e) \({(\frac{1}{5})^{\sqrt 2 }} < {(\frac{1}{5})^{1,4}}\)
g) \({6^\pi } > {6^{3,14}}\).
Bài 2.21: Từ đồ thị của hàm số \(y = {3^x}\) , hãy vẽ đồ thị của các hàm số sau:
a) y = 3x – 2
b) y = 3x + 2
c) y = |3x –2|
d) y = 2 – 3x
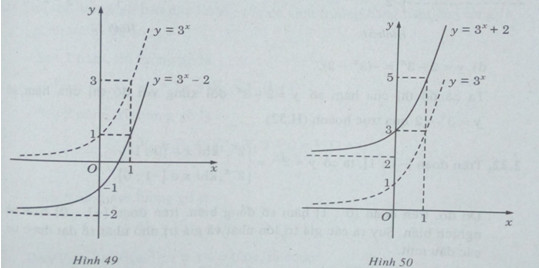
a) Đồ thị của hàm số y \(y = {3^x} – 2\) nhận được từ đồ thị của hàm số \(y = {3^x}\) bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
b) Đồ thị của hàm số \(y = {3^x} + 2\) nhận được từ đồ thị của hàm số \(y = {3^x}\) bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c) \(y = |{3^x} – 2| = \left\{ \begin{array}{l}
{3^x} – 2,{3^x} – 2 \ge 0\\
– {3^x} + 2,{3^x} – 2 < 0
\end{array} \right.\)
Do đó, đồ thị của hàm số \(y = |{3^x} – 2|\) gồm:
– Phần đồ thị của hàm số \(y = {3^x} – 2\) ứng với \({3^x} – 2 \ge 0\) (nằm phía trên trục hoành).
– Phần đối xứng qua trục hoành của đồ thị hàm số \(y = {3^x} – 2\) ứng với \({3^x} – 2 < 0\) .
Vậy đồ thị của hàm số \(y = |{3^x} – 2|\) có dạng như hình 51.
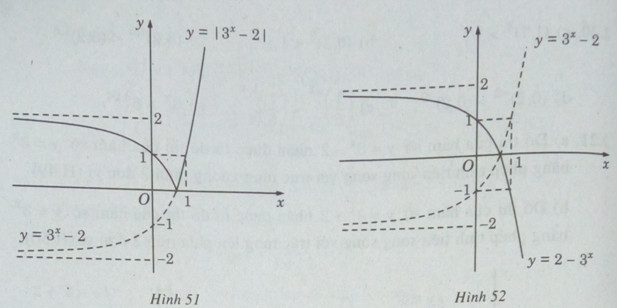d) \(y = 2 – {3^x} = – ({3^x} – 2)\)
Ta có đồ thị của hàm số \(y = 2 – {3^x}\) đối xứng với đồ thị cua hàm số \(y = {3^x} – 2\) qua trục hoành (H.52).
