Bài 68: Chứng minh các bất đẳng thức sau:
a) \(\tan x > x,\,\forall x \in \left( {0;{\pi \over 2}} \right)\);
b) \(\tan x > x + {{{x^3}} \over 3},\,\forall x \in \left( {0;{\pi \over 2}} \right)\)
a) Chứng minh rằng hàm số: \(f\left( x \right) = \tan x – x\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\)
a) Hàm số \(f\left( x \right) = \tan x – x\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và có đạo hàm \(f’\left( x \right) = {1 \over {{{\cos }^2}x}} – 1 > 0\,\,\forall x\left( {0;{\pi \over 2}} \right)\)
Do đó hàm số \(f\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\)
Từ đó: \(f\left( x \right) > f\left( 0 \right)\forall x \in \left( {0;{\pi \over 2}} \right) \)
\(\Leftrightarrow \tan x – x > 0\forall x \in \left( {0;{\pi \over 2}} \right)\)
b) Hàm số \(f\left( x \right) = \tan x – x – {{{x^3}} \over 3}\) liên tục trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và có đạo hàm \(f’\left( x \right) = {1 \over {{{\cos }^2}x}} – 1 = {\tan ^2}x – {x^2} > 0\,\,\forall x\left( {0;{\pi \over 2}} \right)\) (suy ra từ a)).
Do đó hàm số \(f\) đồng biến trên nửa khoảng \(\left[ {0;{\pi \over 2}} \right)\) và khi đó
\(f\left( x \right) = f\left( 0 \right) = 0\,\,\forall x \in \left( {0;{\pi \over 2}} \right)\)
\(\Rightarrow \tan x > x + {{{x^3}} \over 3}\,\,\forall x \in \left( {0;{\pi \over 2}} \right)\)
Bài 69: Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:
a) \(y = \sqrt {3x + 1} \) b) \(y = \sqrt {4x – {x^2}} \)
c) \(y = x + \sqrt x \) d) \(y = x – \sqrt x \)
a)TXĐ: \(D = \left[ { – {1 \over 3}; + \infty } \right)\)
\(y’ = {3 \over {2\sqrt {3x + 1} }} > 0\,\forall x > – {1 \over 3}\)
Advertisements (Quảng cáo)
Hàm số đồng biến \(\left( { – {1 \over 3}; + \infty } \right)\), hàm số không có cực trị.
b) TXĐ: \(D = \left[ {0;4} \right]\)
\(y’ = {{4 – 2x} \over {2\sqrt {4x – {x^2}} }};\,y’ = 0 \Leftrightarrow x = 2;\,y\left( 2 \right) = 2\)
Bảng biến thiên
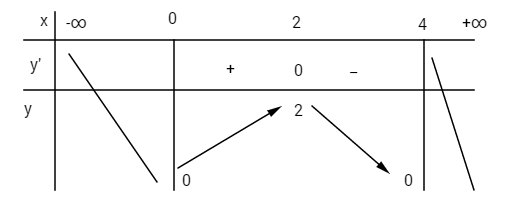
Hàm số đạt cực đại tại điểm \(x = 2\); giá trị cực đại \(y(2) = 2\).
c) TXĐ: \(D = \left[ {0; + \infty } \right)\)
\(\eqalign{
& y’ = 1 + {1 \over {2\sqrt x }} = {{2\sqrt x + 1} \over {2\sqrt x }} \cr
& \cr} \)
\(y’ = 1 + {1 \over {2\sqrt x }} > 0\,\forall x > 0\)
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\), hàm số không có cực trị.
d) TXĐ: \(D = \left[ {0; + \infty } \right)\)
\( y’ = 1 – {1 \over {2\sqrt x }} \)
Advertisements (Quảng cáo)
\(y’ = 0 \Leftrightarrow x = {1 \over 4}\)
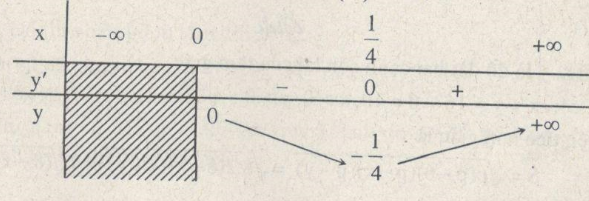
Hàm số đạt cực tiểu tại điểm \(x = {1 \over 4}\); giá trị cực tiểu \(y\left( {{1 \over 4}} \right) = – {1 \over 4}\)
Bài 70: Người ta định làm một cái hộp hình trụ bằng tôn có thể tích \(V\) cho trước. Tìm bán kính đáy \(r\) và chiều cao của hình trụ sao cho tốn ít nguyên liệu nhất.
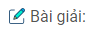
Thể tích của hình trụ là: \(V = B.h = \pi {r^2}.h \Rightarrow h = {V \over {\pi {r^2}}}\)
Diện tích toàn phần của hình trụ là:
\(S = 2\pi {r^2} + 2\pi r.h = 2\pi {r^2} + 2\pi .r.{V \over {\pi {r^2}}} = 2\pi {r^2} + {{2V} \over r}\)
Xét hàm số:
\(\eqalign{
& S\left( r \right) = 2\pi {r^2} + {{2V} \over r}\,\,\left( {r > 0} \right) \cr
& S’ = 4\pi r – {{2V} \over {{r^2}}} = {{4\pi {r^2} – 2V} \over {{r^2}}} \cr
& S’ = 0 \Leftrightarrow r = \root 3 \of {{V \over {2\pi }}} \cr} \)
Bảng biến thiên:
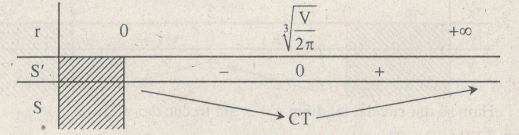
\(S\) đạt giá trị nhỏ nhất tại điểm \(r = \root 3 \of {{V \over {2\pi }}} \) khi đó \(h = {V \over {\pi {r^2}}} = {V \over {\pi \root 3 \of {{{{V^2}} \over {4{\pi ^2}}}} }} = \root 3 \of {{{4V} \over \pi }} \)
Bài 71: Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhât.
Có thể áp dụng công thức Hê-rông để tính diện tích tam giác: Nếu tam giác ABC có độ dài các cạnh là a, b, c thì diện tích của nó là: \(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \) (p là nửa chu vi của tam giác.)
Gọi x, y là độ dài hai cạnh còn lại của tam giác.
Ta có: \(x + y = 16 – 6 = 10,\,x > 0,\,y > 0\)
Diện tích tam giác là: \(S = \sqrt {p\left( {p – 6} \right)\left( {p – x} \right)\left( {p – y} \right)} \)
\(= \sqrt {8.2\left( {8 – x} \right)\left( {8 – y} \right)} = 4\sqrt {\left( {8 – x} \right)\left( {8 – y} \right)} \)
Thay y= 10- x , ta được \(S = 4\sqrt {\left( {8 – x} \right)\left( {x – 2} \right)} \)
\(= 4\sqrt {{-x^2} + 10x – 16} \,\,\,\left( {0 < x < 10} \right)\)
S đạt gía trị lớn nhất trên khoảng (0;10) khi và chỉ khi hàm số \(f\left( x \right) = – {x^2} + 10x – 16\) đạt giá trị lớn nhất trên khoảng (0;10).
\(f’\left( x \right) = – 2x + 10;\,f’\left( x \right) = 0 \Leftrightarrow x = 5;\,f\left( 5 \right) = 9\)
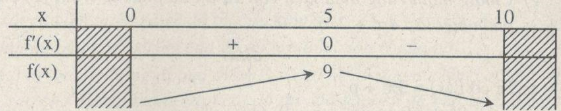
Tam giác có diện tích lớn nhất khi x = 5 (cm) và y= 5 (cm)
\(\mathop {\max }\limits_{x \in \left( {0;10} \right)} f\left( x \right) = f\left( 5 \right) = 9\)
Khi đó diện tích tam giác là: \(S = 4\sqrt 9 = 12\left( {c{m^2}} \right)\)
