Bài 61: Một viên đạn được bắn ra với vận tốc ban đầu \({v_o} > 0\) từ một nòng súng đặt ở gốc tọa độ \(O\), nghiêng một góc \(\alpha \) với mặt đất (nòng súng nằm trong mặt phẳng thẳng đứng \(Oxy\) và tạo với trục hoành \(Ox\) góc \(\alpha \) ). Biết quỹ đạo chuyển động của viên đạn là parabol.
\(\left( {{\gamma _\alpha }} \right):y = – {g \over {2v_o^2}}\left( {1 + {{\tan }^2}\alpha } \right){x^2} + x\tan \alpha \) ( \(g\) là gia tốc trọng trường).
Chứng minh rằng với mọi \(\alpha \in \left( {0;{\pi \over 2}} \right),\,\left( {{\gamma _\alpha }} \right)\) luôn tiếp xúc với parabol \((P)\) có phương trình là: \(y = – {g \over {2v_o^2}}{x^2} + {{v_o^2} \over {2g}}\) và tìm tọa độ tiếp điểm \((P)\) được gọi là parabol an toàn).
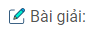
Hoành độ tiếp điểm của hai parabol là nghiệm của hệ phương trình:
\(\left\{ \matrix{
– {g \over {2v_o^2}}\left( {1 + {{\tan }^2}\alpha } \right){x^2} + x\tan \alpha = – {g \over {2v_o^2}}{x^2} + {{v_o^2} \over {2g}} \hfill \cr
– {g \over {v_o^2}}\left( {1 + {{\tan }^2}\alpha } \right)x + \tan \alpha = – {g \over {v_o^2}}x \hfill \cr} \right.\)
Nghiệm của phương trình thứ hai của hệ là \(x = {{v_o^2} \over {g\tan \alpha }}\)
Ta có \(x = {{v_o^2} \over {g\tan \alpha }}\) cũng là nghiệm của phương trình thứ nhất của hệ. Vậy với mọi \(\alpha \in \left( {0;{\pi \over 2}} \right)\) hai parabol luôn tiếp xúc với nhau. Hoành độ tiếp điểm là \(x = {{v_o^2} \over {g\tan \alpha }}\). Tung độ của tiếp điểm là
\(y = – {g \over {2v_o^2}}{\left( {{{v_o^2} \over {g\tan \alpha }}} \right)^2} + {{v_o^2} \over {2g}} = {{v_o^2} \over {2g}}\left( {1 – {1 \over {{{\tan }^2}\alpha }}} \right)\)
Điểm \(\left( {{{v_o^2} \over {g\tan \alpha }};{{v_o^2} \over {2g}}\left( {1 – {{\cot }^2}\alpha } \right)} \right)\) là tiếp điểm của hai parabol với mọi \(\alpha \in \left( {0;{\pi \over 2}} \right)\)
Bài 62: a) Khảo sát sự biến thiên và vẽ đồ thị hàm số: \(y = {{x – 1} \over {x + 1}}\)
b) Chứng minh rằng giao điểm \(I\) của hai đường tiệm cận của đường cong đã cho là tâm đối xứng của nó.
Giải
Tập xác định:
\(\eqalign{
& D = R\backslash \left\{ { – 1} \right\} \cr
& \cr} \)
Sự biến thiên:
\(y’ = {2 \over {{{(x + 1)}^2}}} > 0\,\forall x \in D\)
Hàm số đồng biến trên khoảng \(( – \infty ; – 1)\) và \(( – 1; + \infty )\)
Giới hạn:
\(\mathop {\lim y}\limits_{x \to – {1^ – }} = + \infty ;\,\mathop {\lim y}\limits_{x \to – {1^ + }} = – \infty \)
Tiệm cận đứng: \(x=-1\)
\(\mathop {\lim y}\limits_{x \to \pm \infty } = 1\)
Tiệm cận ngang: \(y=1\)
Bảng biến thiên:
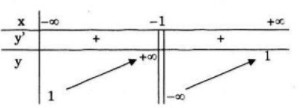
Đồ thị giao \(Ox\) tại điểm \((1;0)\)
Đồ thị giao \(Oy\) tại điểm \((0;-1)\)
Advertisements (Quảng cáo)
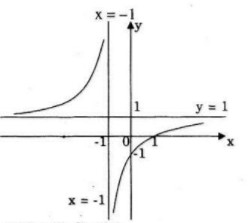
b) Giao điểm của hai tiệm cận của đường cong là \(I(-1;1)\)
Công thức đổi trục tịnh tiến theo vecto \(\overrightarrow {OI} \) là
\(\left\{ \matrix{
x = X – 1 \hfill \cr
y = Y + 1 \hfill \cr} \right.\)
Phương trình đường cong trong hệ tọa độ \(IXY\) là:
\(Y + 1 = {{X – 1 – 1} \over {X – 1 + 1}} \Leftrightarrow Y + 1 = {{X – 2} \over X} \Leftrightarrow Y = – {2 \over X}\)
Đây là hàm số lẻ nên đồ thị nhận gốc \(I\) làm tâm đối xứng.
Bài 63: a) Khảo sát sự biến thiên và vẽ đồ thị \((H)\) của hàm số: \(y = {{x + 2} \over {2x + 1}}\)
b) Chứng minh rằng đường thẳng \(y = mx + m – 1\) luôn đi qua một điểm cố định của đường cong (H) khi m biến thiên.
c) Tìm các giá trị của m sao cho đường thẳng đã cho cắt đường cong \((H)\) tại hai điểm thuộc cùng một nhánh của (H).
a) Tập xác định: \(D =\mathbb R\backslash \left\{ { – {1 \over 2}} \right\}\)
+) Sự biến thiên:
\(y’ = {{ – 3} \over {{{(2x + 1)}^2}}} < 0\,\forall x \in D\)
Hàm số nghịch biến trên khoảng \(\left( { – \infty ; – {1 \over 2}} \right)\) và \(\left( { – {1 \over 2}; + \infty } \right)\)
Giới hạn:
\(\mathop {\lim y}\limits_{x \to – {{{1 \over 2}}^ – }} = – \infty ;\,\mathop {\lim y}\limits_{x \to – {{{1 \over 2}}^ + }} = + \infty \)
Hầm số không có cực trị.
Advertisements (Quảng cáo)
Tiệm cận đứng: \(x={ – {1 \over 2}}\)
\(\mathop {\lim y}\limits_{x \to \pm \infty } = {1 \over 2}\)
Tiệm cận ngang \(y={1 \over 2}\)
Bảng biến thiên:
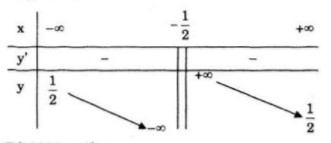
Đồ thị giao \(Ox\) tại điểm \((-2;0)\)
Đồ thị giao \(Oy\) tại điểm \((0;2)\)
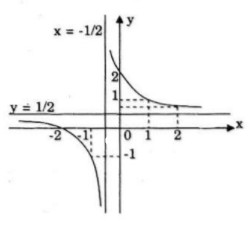
b) Ta có \(y = mx + m – 1 \Leftrightarrow y + 1 = m\left( {x + 1} \right)\)
Tọa độ điểm cố định \(A\) của đường thẳng là nghiệm của hệ:
\(\left\{ \matrix{
x + 1 = 0 \hfill \cr
y + 1 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = – 1 \hfill \cr
y = – 1 \hfill \cr} \right.\)
Vậy \(A(-1;1)\)
Tọa độ \(A\) thỏa mãn phương trình \(y = {{x + 2} \over {2x + 1}}\) nên \(A\) thuộc đường cong \((H)\).
c) Hoành độ giao điểm của đường thẳng đã cho và đường cong \((H)\) là nghiệm của phương trình:
\(\eqalign{
& \,\,\,m\left( {x + 1} \right) – 1 = {{x + 2} \over {2x + 1}}\cr& \Leftrightarrow \left( {2x + 1} \right)\left[ {m\left( {x + 1} \right) – 1} \right] = x + 2 \cr
& \Leftrightarrow m\left( {x + 1} \right)\left( {2x + 1} \right) – \left( {2x + 1} \right) = x + 2 \cr
& \Leftrightarrow \left( {x + 1} \right)\left( {2mx + m – 3} \right) = 0 \cr&\Leftrightarrow \left[ \matrix{
x = – 1 \hfill \cr
f\left( x \right) = 2mx + m – 3 = 0\,\,\,\left( 1 \right) \hfill \cr} \right. \cr} \)
Hai nhánh của \((H)\) nằm về hai bên của tiệm cận đứng \(x = – {1 \over 2}\)
Điểm \(A(-1;1)\) thuộc nhánh trái của \((H)\) vì \({x_A} = – 1 < – {1 \over 2}\)
Đường thẳng cắt \((H)\) tại hai điểm thuộc cùng một nhánh khi và chỉ khi (1) có nghiệm \(x < – {1 \over 2}\) và \(x \ne – 1\) tức
\(\left\{ \matrix{
x \ne 0 \hfill \cr
x = {{ – m + 3} \over 2} < – {1 \over 2} \hfill \cr
f\left( { – 1} \right) \ne 0 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
m \ne 0 \hfill \cr
{3 \over {2m}} < 0 \hfill \cr
– m – 3 \ne 0 \hfill \cr} \right. \)
\(\Leftrightarrow m < – 3\,\, \text{hoặc}\, – 3 < m < 0.\)
Bài 64: Cho hàm số \(y = {{a{x^2} – bx} \over {x – 1}}\)
a) Tìm \(a\) và \(b\) biết rằng đồ thị \((C)\) của hàm số đã cho đi qua điểm \(A\left( { – 1;{5 \over 2}} \right)\) và tiếp tuyến của \((C)\) tại điểm \(O(0;0)\) có hệ số bằng \(-3\).
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị của \(a\) và \(b\) đã tìm được.
a) Ta có: \({M_o} \in \left( C \right)\) \(y’ = {{\left( {12ax – b} \right)\left( {x – 1} \right) – \left( {a{x^2} – bx} \right)} \over {{{\left( {x – 1} \right)}^2}}}\)
Đồ thị \((C)\) đi qua \(A\left( { – 1;{5 \over 2}} \right)\) \( \Leftrightarrow y\left( { – 1} \right) = {5 \over 2} \Leftrightarrow {{a + b} \over { – 2}} = {5 \over 2} \Leftrightarrow a + b = – 5\,\,\,\left( 1 \right)\)
Tiếp tuyến của \((C)\) tại \(O(0;0)\) có hệ số góc bằng \(-3\) khi và chỉ khi \(y’(0) = -3 \)\( \Leftrightarrow b = – 3\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(a = -2; b = – 3\).
b) Với \(a = -2; b = – 3\) ta có: \(y = {{ – 2{x^3} + 3x} \over {x – 1}}\)
Tập xác định: \(D = \mathbb R\backslash \left\{ 1 \right\}\)
\(y’ = {{ – 2{x^2} + 4x – 3} \over {{{(x – 1)}^2}}} < 0\,\forall x \in D\)
Hàm số nghịch biến trên khoảng: \(( – \infty ;1)\) và \((1; + \infty )\)
Hàm số không có cực trị
Giới hạn:
\(\mathop {\lim y}\limits_{x \to {1^ – }} = – \infty ;\,\mathop {\lim y}\limits_{x \to {1^ + }} = + \infty \)
Tiệm cận đứng là: \(x=1\)
\(\eqalign{
& a = \mathop {\lim }\limits_{x \to \infty } {y \over x} = \mathop {\lim }\limits_{x \to \infty } {{ – 2{x^2} + 3x} \over {{x^2} – x}} = – 2 \cr
& b = \mathop {\lim }\limits_{x \to \infty } (y + 2x) = \mathop {\lim }\limits_{x \to \infty } \left( {{{ – 2{x^2} + 3x} \over {x – 1}} + 2x} \right) = 1 \cr} \)
Tiệm cận xiên là: \(y=-2x+1\)
Bảng biến thiên:
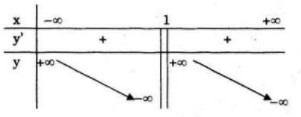
Đồ thị giao \(Oy\) tại điểm \((0;0)\) và \(\left( {{3 \over 2};0} \right)\)