Bài 16: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(f\left( x \right) = {\sin ^4}x + {\cos ^4}x\)
TXĐ: \(D=\mathbb R\)
\(\eqalign{
& f\left( x \right) = {\left( {{{\sin }^2}x} \right)^2} + {\left( {{{\cos }^2}x} \right)^2} + 2{\sin ^2}x{\cos ^2}x \cr&\,\,\,\,\,\,\,\,\,\,\,\;\;\;\;- 2{\sin ^2}x{\cos ^2}x \cr
& \,\,\,\,\,\,\,\,\,\,\,\;\; = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} – 2{\sin ^2}x{\cos ^2}x \cr&\,\,\,\,\,\,\,\,\,\,\,\;\;= 1 – {1 \over 2}{\sin ^2}2x \cr} \)
Vì \(0 \le {\sin ^2}2x \le 1\) nên: \(\,\,f\left( x \right) \le 1\) với mọi \(x \in {\mathbb{R}},f\left( 0 \right) = 1\). Vậy \(\mathop {\max f\left( x \right)}\limits_{x \in {\mathbb {R}}} = 1\)
\(*\,\,\,f\left( x \right) \ge {1 \over 2}\) với mọi \(x \in {\mathbb{R}},f\left( {{\pi \over 4}} \right) = 1 – {1 \over 2} = {1 \over 2}\)
Vậy \(\mathop {\min f\left( x \right)}\limits_{x \in {\mathbb {R}}} = {1 \over 2}\).
Bài 17: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(f\left( x \right) = {x^2} + 2x – 5\) trên đoạn \(\left[ { – 2;3} \right]\);
b) \(f\left( x \right) = {{{x^3}} \over 3} + 2{x^2} + 3x – 4\) trên đoạn \(\left[ { – 4;0} \right]\);
c) \(f\left( x \right) = x + {1 \over x}\) trên đoạn \(\left( {0; + \infty } \right)\);
d) \(f\left( x \right) = – {x^2} + 2x + 4\) trên đoạn \(\left[ {2;4} \right]\);
e) \(f\left( x \right) = {{2{x^2} + 5x + 4} \over {x + 2}}\) trên đoạn \(\left[ {0;1} \right]\);
f) \(f\left( x \right) = x – {1 \over x}\) trên đoạn \(\left( {0;2} \right]\);
a) \(D = \left[ { – 2;3} \right];f’\left( x \right) = 2x + 2;f’\left( x \right) = 0\)
\(\Leftrightarrow x=- 1 \in \left[ { – 2;3} \right]\)
Ta có: \(f\left( { – 2} \right) = – 5;f\left( { – 1} \right) = – 6;f\left( 3 \right) = 10\).
Vậy: \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { – 2;3} \right]} = – 6;\,\,\,\,\,\,\mathop {\max \,f\left( x \right) = 10}\limits_{x \in \left[ { – 2;3} \right]} \).
Advertisements (Quảng cáo)
b)
\(D = \left[ { – 4;0} \right];\,f’\left( x \right) = {x^2} + 4x + 3;f’\left( x \right) = 0\)
\(\Leftrightarrow \left[ \matrix{
x = – 1 \in \left[ { – 4;0} \right] \hfill \cr
x = – 3 \in \left[ { – 4;0} \right] \hfill \cr} \right.\)
Ta có: \(f\left( { – 4} \right) = – {{16} \over 3};f\left( { – 1} \right) = – {{16} \over 3};\)
\(f\left( { – 3} \right) = – 4;f\left( 0 \right) = – 4\)
Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ { – 4;0} \right]} = – {{16} \over 3};\,\,\mathop {\max \,f\left( x \right)}\limits_{x \in \left[ { – 4;0} \right]} = – 4\).
c) \(D = \left( {0; + \infty } \right);f’\left( x \right) = 1 – {1 \over {{x^2}}} = {{{x^2} – 1} \over {{x^2}}}\)với mọi \(x \ne 0,f’\left( x \right) = 0 \Leftrightarrow x = \pm 1\)
\(x=1\in \left\{ {0; + \infty } \right.)\)
\(x=-1\not\in \left\{ {0; + \infty } \right.)\)
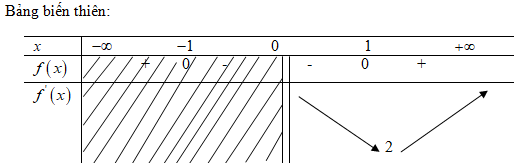
\(\mathop {\min \,\,f\left( x \right) = f\left( 1 \right)}\limits_{x \in \left( {0; + \infty } \right)} = 2\). Hàm số không đạt giá trị lớn nhất trên khoảng \(\left( {0; + \infty } \right)\).
d) \(D = \left[ {2;4} \right];f’\left( x \right) = – 2x + 2;f’\left( x \right) = 0 \)
Advertisements (Quảng cáo)
\(\Leftrightarrow x = 1 \notin \left[ {2;4} \right]\)
Ta có: \(f\left( 2 \right) = 4;f\left( 4 \right) = – 4\)
Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = – 4;\,\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {2;4} \right]} = 4\).
e)
\(D = \left[ {0;1} \right];f’\left( x \right) = {{2{x^2} + 8x + 6} \over {{{\left( {x + 2} \right)}^2}}};f’\left( x \right) = 0\)
\(\Leftrightarrow \left[ \matrix{
x = – 1 \notin \left[ {0;1} \right] \hfill \cr
x = – 3 \notin \left[ {0;1} \right] \hfill \cr} \right.\)
Ta có: \(f\left( 0 \right) = 2;f\left( 1 \right) = {{11} \over 3}\)
Vậy \(\mathop {\min \,f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = 2;\) \(\mathop {\max f\left( x \right)}\limits_{x \in \left[ {0;1} \right]} = {{11} \over 3}\)
f) \(D = \left( {0;2} \right];f’\left( x \right) = 1 + {1 \over {{x^2}}} > 0\) với mọi \(x \in \left( {0;2} \right];f\left( 2 \right) = {3 \over 2}\)
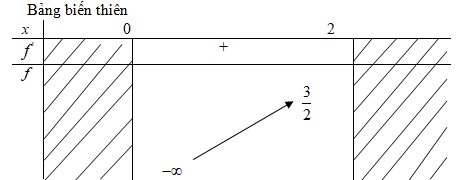
\(\mathop {\,\max f\left( x \right)}\limits_{x \in \left[ {0;2} \right]} = {3 \over 2}\) . Hàm số không đạt giá trị nhỏ nhất trên \(\left( {0;2} \right]\).
Bài 18: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = 2{\sin ^2}x + 2\sin x – 1\)
b) \(y = {\cos ^2}2x – \sin x\cos x + 4\)
a) Đặt \(t = \sin x, – 1 \le t \le 1\)
\(y = f\left( t \right) = 2{t^2} + 2t – 1\)
Ta tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( t \right)\) trên đoạn \(\left[ { – 1;1} \right]\). Đó cũng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên \(\mathbb R\).
\(f’\left( t \right) = 4t + 2;f’\left( t \right) = 0 \Leftrightarrow t = – {1 \over 2}\)
Ta có: \(f\left( { – 1} \right) = – 1;f\left( { – {1 \over 2}} \right) = – {3 \over 2};f\left( 1 \right) = 3\)
\(\mathop {\min \,\,f\left( t \right)}\limits_{t \in \left[ { – 1;1} \right]} = – {3 \over 2};\,\,\,\,\,\,\mathop {\max \,\,f\left( t \right)}\limits_{t \in \left[ { – 1;1} \right]} = 3\)
Vậy \(\mathop {\min \,\,y}\limits_{x \in {\mathbb{R}}} = – {3 \over 2};\,\,\,\,\,\,\mathop {\max \,\,y}\limits_{x \in {\mathbb{R}}} = 3\).
b) Ta có: \(y = 1 – {\sin ^2}2x – {1 \over 2}\sin 2x + 4\)
\(= – {\sin ^2}2x – {1 \over 2}\sin 2x + 5\)
Đặt \(t = \sin 2x, – 1 \le t \le 1\)
\(y = f\left( t \right) = – {t^2} – {1 \over 2}t + 5;f’\left( t \right) = – 2t – {1 \over 2};\)
\(f’\left( t \right) = 0 \Leftrightarrow t = – {1 \over 4} \in \left[ { – 1;1} \right]\)
Ta có: \(f\left( { – 1} \right) = {9 \over 2};f\left( { – {1 \over 4}} \right) = {{81} \over {16}};f\left( 1 \right) = {7 \over 2}\)
\(\mathop {\min \,\,f\left( t \right)}\limits_{t \in \left[ { – 1;1} \right]} = {7 \over 2};\,\,\,\,\,\mathop {\max \,\,f\left( t \right)}\limits_{t \in \left[ { – 1;1} \right]} = {{81} \over {16}}\)
Vậy \(\mathop {\min \,\,y}\limits_{x \in {\mathbb{R}}} = {7 \over 2};\,\,\,\,\,\mathop {\max \,\,y}\limits_{x \in {\mathbb{R}}} = {{81} \over {16}}\).

