Bài 1.27: Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x = 2\sqrt 2 \). Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \(k = {1 \over 2}\) và phép quay tâm O góc 45°
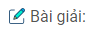
Gọi \(d_1\) là ảnh của d qua phép vị tự tâm O tỉ số \(k = {1 \over 2}\) thì phương trình của \(d_1\) là \(x = \sqrt 2 \). Giả sử d’ là ảnh của d qua phép quay tâm O góc 45°. Lấy \(M\left( {\sqrt 2 ;0} \right)\) thuộc \(d_1\) thì ảnh của nó qua phép quay tâm O góc 45° là \(M’\left( {1;1} \right)\) thuộc d’. Vì \(OM \bot {d_1}\) nên \(OM’ \bot d’\). Vậy d’ là đường thẳng đi qua M’ và vuông góc với OM’. Do đó nó có phương trình \(x + y – 2 = 0\).
Bài 1.28: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình \({\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} = 4\). Hãy viết phương trình đường tròn (C’) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = -2 và phép đối xứng qua trục Ox.
Dễ thấy bán kính của (C’) = 4. Tâm I của (C’) là ảnh của tâm \(I\left( {1;2} \right)\) của (C) qua phép đồng dạng nói trên. Qua phép vị tự tâm O tỉ số k = -2 , I biến thành \({I_1}\left( { – 2; – 4} \right)\). Qua phép đối xứng qua trục Ox, \(I_1\) biến thành \(I’\left( { – 2;4} \right)\).
Từ đó suy ra phương trình của (C’) là \({\left( {x + 2} \right)^2} + {\left( {y – 4} \right)^2} = 16\).
Advertisements (Quảng cáo)
Bài 1.29: Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau
Dùng phép tịnh tiến đưa về hai đa giác đều cùng tâm đối xứng, sau đó dùng phép quay đưa về hai đa giác đều cùng tâm đối xứng có các đỉnh tương ứng thẳng hàng với tâm, cuối cùng dùng phép tịnh tiến tự biến đa giác này thành đa giác kia.
Bài 1.30: Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo.
Advertisements (Quảng cáo)
a) Tìm tập hợp các điểm C khi D thay đổi
b) Tìm tập hợp các điểm I khi C và D thay đổi như trong câu a) .
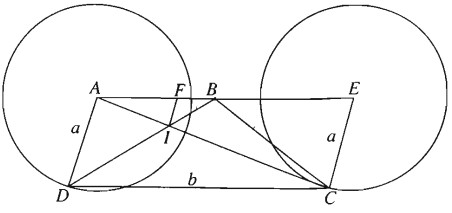
a) Dựng hình bình hành ADCE. Ta có \(\overrightarrow {DC} = \overrightarrow {A{\rm{E}}}\) không đổi.
Do AE = b không đổi, nên E cố định. Do \(A{\rm{D}} = EC = a\) nên khi D chạy trên đường tròn \(\left( {A;a} \right)\) thì C chạy trên đường tròn \(\left( {E;a} \right)\) là ảnh của \(\left( {A;a} \right)\) qua phép tịnh tiến theo \(\overrightarrow {A{\rm{E}}} \).
b) Đường thẳng qua I, song song với AD cắt AE tại F.
Ta có
\(\eqalign{
& {{AI} \over {IC}} = {{AB} \over {C{\rm{D}}}} \cr
& \Rightarrow {{AI} \over {AI + IC}} = {{AB} \over {AB + b}} \cr
& \Rightarrow {{AI} \over {IC}} = {{AB} \over {AB + b}} \cr
& \overrightarrow {AI} = {{AB} \over {AB + b}}\overrightarrow {AC} \cr} \)
Do đó có thể xem I là ảnh của C qua phép vị tự tâm A, tỉ số \({{AB} \over {AB + b}}\). Vậy khi C chạy trên (E;a) thì I chạy trên đường tròn là ảnh của (E;a) qua phép vị tự nói trên.

