Câu C1: Khi một tia sáng đi từ môi trường này đến môi trường khác, chiết suất tỉ đối của hai môi trường cho ta biết gì về đường đi của tia sáng đó?
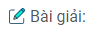
Khi một tia sáng đi từ môi trường này sang môi trường khác, để vẽ được tia khúc xạ, ta cần phải biết chiết suất của hai môi trường.
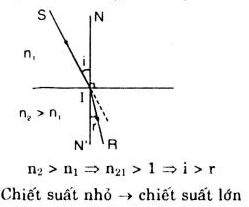
Bài 1: Chọn câu đúng.Chiết suất tí đối giữa môi trương khúc xạ và môi trường tới
A. luôn lớn hơn 1.
B. luôn nhỏ hơn 1.
C. bằng tỉ số giữa chiết suất tuyệt đối của môi trường khúc xạ và chiết suất tuyệt đối của môi trường tới.
D. bằng hiệu số giữa chiết suất tuyệt đối của môi trường khúc xạ và chiết suất tuyệt đối của môi trường tới.
Chọn C. Ta có \({n_{21}} = {{{n_2}} \over {{n_1}}}\)
Câu C2: Một người nhìn thấy con cá ở trong nước. Hỏi muốn đâm trúng con cá thì người đó phải phóng mùi lao vào chỗ nào, đúng vào chỗ người đó nhìn thấy con cá, lấy ở phía trên, phía dưới chỗ đó? Giải thích.
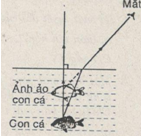
Một người đứng trên thuyền nhìn xuống mặt nưốc theo phương gần như thẳng góc với mặt nước nhìn thấy con cá ở trong nước, đó chỉ là ta thấy ảnh ảo của con cá, con cá thật nằm ở độ sâu hơn, do đó phải phóng mũi lao vào phía dưới chỗ nhìn thấy thì mới trúng con cá thật.
Bài 2: Chọn câu đúng.
Chiết suất tuyệt đối của một môi trường truyền sáng
A. luôn lớn hơn 1 B. luôn nhỏ hơn 1.
C.bằng 1. D. luôn lớn hơn 0.
Chọn A
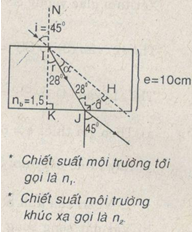
Bài 3: Một bản mặt song song (một bản trong suốt giới hạn bởi hai mặt pỉiẳng song song) có bể dày 10cm, chiết suất n = 1,5 được đặt trong không khí. Chiếu tới bản một tia sáng SI có góc tới là 45°.
a) Chứng tỏ ràng tia sáng ló ra khỏi bân có phương song song với tia tới. Vẽ đường đi của tia sáng qua bản.
b) Tính khoảng cách giữa giá của tia ló và tia tới.
Advertisements (Quảng cáo)
a) Không khí (n1) —> bản song song (n2):
Trước hết tia sáng đi từ không khí vào bản song song; ta có khúc xạ cụp, vì nkk< nb
Theo định luật khúc xạ ánh sáng
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{n_1}\sin i} \over {{n_2}}}\)
Thay số: \({\mathop{\rm s}\nolimits} {\rm{inr = }}{{1\sin {{45}^0}} \over {1,5}} = 0,47 \Rightarrow r = {28^0}\)
Bản song song -> không khí:
Theo tínn truyền thuận nghịch của tia sáng, ta có góc tới i = 28° thì góc khúc xạ là r = 45° nên tia ló ra khỏi bản sẽ song song với tia tới.
b) Gọi d là khoảng cách giữa giá của tia tới và tia ló, d = JH.
Xét tam giác vuông IKJ:
\({\rm{cos\,r = }}{{IK} \over {IJ}} \Rightarrow {\rm{I}}J = {{IK} \over {{\rm{cos\,r}}}} = {e \over {{\rm{cos\,r}}}}\)
Xét tam giác vuông IHJ:
\(\sin \alpha = sin\left( {i – r} \right) = {{JH} \over {IJ}} \Rightarrow JH = IJsin\left( {i – r} \right)\)
\( \Rightarrow d = {e \over {{\rm{cos\,r}}}}\sin \left( {i – r} \right)\)
(công thức tính khoảng cách giữa giá của tia ló là tia tới của bản song song).
Thay số:
\(d = {{10} \over {{\rm{cos2}}{{\rm{8}}^0}}}\sin \left( {{{45}^0} – {{28}^0}} \right) = 3,3\left( {cm} \right)\)
Bài 4: Một bản mặt song song có bề dày 6cm, chiết suất n = 1,5, được đặt trong không khí.
Advertisements (Quảng cáo)
a) Vật là một điểm sáng S cách bản 20cm. Xác định vị trí của ảnh.
b) Vật AB = 2 cm đặt song song với bản. Xác định vị trí và độ lớn của ảnh.
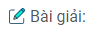
Công thức tính độ dời của ảnh: xét chùm tia sáng tới hẹp gần như vuông góc với bản mặt song song. Lúc đó góc tới i và góc khúc xạ r đều rất nhỏ nên có thể dùng các công thức gần đúng.
\(\sin i \approx i\,;\cos r \approx {\rm{1}}\)
Do đó: \({{\sin i} \over {{\mathop{\rm s}\nolimits} {\rm{inr}}}} = n \Rightarrow {i \over r} = n\,\,\,\,hay\,\,\,\,{r \over i} = {1 \over n}\)(1)
Ta lại có: \(d = {e \over {{\rm{cos}}\,{\rm{r}}}}\sin \left( {i – r} \right)\) (2)
Xét tam giác vuông SS’H: \(\sin i = {d \over {SS’}} \Rightarrow SS’ = {d \over {\sin i}}\)(3)
Thế (2) vào (3)
\(SS’ = {{e\sin \left( {i – r} \right)} \over {{\rm{cos}}\,{\rm{r}}\sin i}} = {{e\left( {i – r} \right)} \over i} = e\left( {1 – {r \over i}} \right)\) (4)
Thế (1) vào (4) ta được: \(SS’ = e\left( {1 – {1 \over n}} \right)\)(Công thức tính độ dời của ảnh).
a) Theo giả thiết e = 6cm, n = 1,5, SH = 20cm
Suy ra độ dời ảnh: \(SS’ = e\left( {1 – {1 \over n}} \right) = 6\left( {1 – {1 \over {1,5}}} \right) = 2\left( {cm} \right)\)
Vậy vị trí của ảnh cách bản mặt song song là S’H = 20 – 2 = 18 (cm)
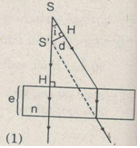
b) Vật đặt song song với bản thì ta có ảnh ảo A’B’ = AB = 2 cm và ảnh dời đi một đoạn
\(BB’ = e\left( {1 – {1 \over n}} \right)\)
\( \Rightarrow BB’ = 6\left( {1 – {1 \over {1,5}}} \right) = 2\left( {cm} \right)\)
Vậy vị trí của ảnh cách bản mặt song song là 18 cm
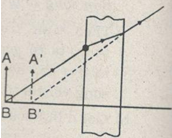
Bài 5: Một cái chậu đặt trên một mặt phẳng nằm ngang, chứa một lớp nước dày 20 cm, chiết suất \(n = {4 \over 3}\). Đáy chậu là một gương phẳng. Mặt M cách mặt nước 30 cm, nhìn thẳng góc xuống đáy chậu. Xác định khoảng cách từ ảnh của mắt tới mặt nước. Vẽ đường đi của ánh sáng qua quang hệ trên.
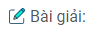
Để giải bài toán này, trước hết ta tìm công thức xác định vật và ảnh của hệ hai môi trường trong suốt (thường là một lưỡng chất phẳng). Ta xét chùm tia sáng hẹp gần như vuông góc với mặt lưỡng chất.
Ta có: \(\tan i = {{IH} \over {SH}} \approx \sin i\) (vì là góc nhỏ)
\({\mathop{\rm t}\nolimits} {\rm{anr}} = {{IH} \over {S’H}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}}\) (vì là góc nhỏ)
\( \Rightarrow {{\sin i} \over {\sin \,r}} = {{S’H} \over {SH}} = {{{n_2}} \over {{n_1}}}\)
Suy ra \({{S’H} \over {{n_2}}} = {{SH} \over {{n_1}}}\) (Công thức này đúng cho mọi trường hợp)
Trở lại bài toán, ta có hình vẽ sau:
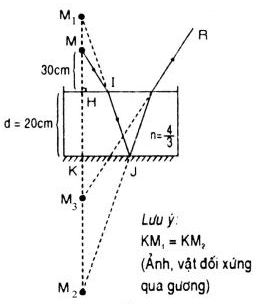
Xét trường hợp ánh sáng đi từ không khí (n1=1) vào nước (\({n_2} = {4 \over 3}\))
Theo công thức trên:\({{{M_1}H} \over {{n_2}}} = {{MH} \over {{n_1}}}\)
\( \Rightarrow {{MH} \over 1} = {{{M_1}H} \over {{4 \over 3}}}\)
\( \Rightarrow {M_1}H = {4 \over 3}MH = {4 \over 3}.30 = 40\,cm\)
Gọi M2 là ảnh ảo của mắt M qua gương phẳng đáy chậu, ta có M2 đối xứng với M1 qua gương:
\(K{M_2} = K{M_1} = KH + H{M_1} = 20+40=60\left( {cm} \right)\)
Xét trường hơp tia sáng phản xa đi từ nước ( \({n_1} = {4 \over 3}\)) ra không khí
(n2 = 1), ta có M3 là ảnh của M2, M3 là ảnh của mắt mà mắt thấy được.
Theo công thức trên:
\({{H{M_3}} \over {{n_2}}} = {{H{M_2}} \over {{n_1}}} \Rightarrow {{H{M_3}} \over 1} = {{H{M_2}} \over {{4 \over 3}}} = {3 \over 4}\left( {H{M_2}} \right) = {3 \over 4}\left( {HK + K{M_2}} \right)\)
\(\; \Rightarrow {\rm{ }}H{M_3} = {3 \over 4}(20 + {\rm{ }}60){\rm{ }} = {\rm{ }}60{\rm{ }}\left( {cm} \right)\)
Vậy khoảng cách từ ảnh M3 đến mặt nước là 60 (cm)

