Bài Đề toán tổng hợp chương III phần hình học Sách bài tập Toán Hình Học 10. Giải bài 3.66, 3.67, 3.68 trang 164 Sách bài tập (SBT) Toán Hình Học 10. Câu 3.66: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có…
Bài 3.66: Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm \(I\left( {{1 \over 2};0} \right)\) phương trình đường thẳng AB là : x – 2y + 2 = 0 và AB = 2AD. Tìm tọa độ các đỉnh A, B, C, D biết rằng đỉnh A có hoành độ âm.

(Xem hình 3.24)
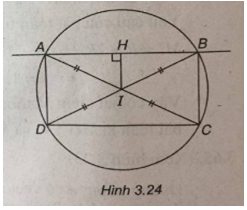
Khoảng cách từ I đến đường thẳng AB bằng
\({{\sqrt 5 } \over 2}\) \(\Rightarrow AD = \sqrt 5 \) và \(IA = IB = {5 \over 2}.\)
Do đó A, B là các giao điểm của đường thẳng AB với đường tròn tâm I và bán kính \(R = {5 \over 2}.\)
Vậy tọa độ A, B là nghiệm của hệ :
\(\left\{ \matrix{
x – 2y + 2 = 0 \hfill \cr
{\left( {x – {1 \over 2}} \right)^2} + {y^2} = {\left( {{5 \over 2}} \right)^2} \hfill \cr} \right.\)
Giải hệ ta được \(A( – 2;0),B(2;2)\) (vì \({x_A} < 0\))
\( \Rightarrow C\left( {3;0} \right),D\left( { – 1; – 2} \right).\)
Bài 3.67: Trong mặt phẳng tọa độ Oxy,xét tam giác ABC vuông tại A, phương trình đường thẳng BC là : \(\sqrt 3 x – y – \sqrt 3 = 0\), các đỉnh A và B thuộc trục hoành và bán kính đường tròn nội tiếp tam giác bằng 2. Tìm tọa độ trọng tâm G của tam giác ABC.

Advertisements (Quảng cáo)
( Xem hình 3.25)
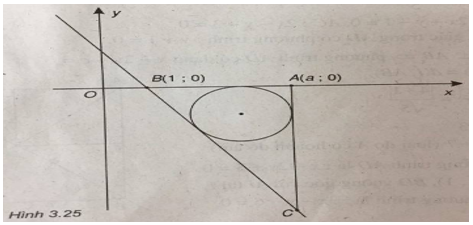
Ta có: \(BC \cap Ox = B(1;0)\)
Đặt \({x_A} = a\) ta có A(a;0) và \({x_C} = a \Rightarrow {y_C} = \sqrt 3 a – \sqrt 3 .\)
Vậy \(C\left( {a;\sqrt 3 a – \sqrt 3 } \right).\)
Từ công thức \(\left\{ \matrix{
{x_G} = {1 \over 3}\left( {{x_A} + {x_B} + {x_C}} \right) \hfill \cr
{y_G} = {1 \over 3}\left( {{y_A} + {y_B} + {y_C}} \right) \hfill \cr} \right.\)
Ta có: \(G\left( {{{2a + 1} \over 3};{{\sqrt 3 \left( {a – 1} \right)} \over 3}} \right).\)
Advertisements (Quảng cáo)
Mà \(AB = \left| {a – 1} \right|,AC = \sqrt 3 \left| {a – 1} \right|,BC = 2\left| {a – 1} \right|\). Do đó :
\({S_{\Delta ABC}} = {1 \over 2}AB.AC = {{\sqrt 3 } \over 2}{\left( {a – 1} \right)^2}.\)
Ta có: \(\eqalign{
& r = {{2S} \over {AB + AC + BC}} \cr
& = {{\sqrt 3 {{\left( {a – 1} \right)}^2}} \over {3\left| {a – 1} \right| + \sqrt 3 \left| {a – 1} \right|}} = {{\left| {a – 1} \right|} \over {\sqrt 3 + 1}} = 2. \cr} \)
Vậy \(\left| {a – 1} \right| = 2\sqrt 3 + 2.\)
Trường hợp 1.
\({a_1} = 2\sqrt 3 + 3 \Rightarrow {G_1}\left( {{{7 + 4\sqrt 3 } \over 3};{{6 + 2\sqrt 3 } \over 3}} \right).\)
Trường hợp 2.
\({a_2} = – 2\sqrt 3 – 1 \Rightarrow {G_2}\left( {{{4\sqrt 3 – 1} \over 3};{{ – 6 – 2\sqrt 3 } \over 3}} \right).\)
Bài 3.68: Trong mặt phẳng tọa độ Oxy, cho điểm C(2;0) và elip (E): \({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\). Tìm tọa độ các điểm A, B thuộc (E), biết rằng hai điểm A, B đối xứng với nhau qua trục hoành và tam giác ABC là tam giác đều.

Giả sử \(A\left( {{x_0};{y_0}} \right)\). Do A, B đối xứng nhau qua Ox nên \(B({x_0}; – {y_0})\)
Ta có : \(A{B^2} = 4y_0^2\) và \(A{C^2} = {\left( {{x_0} – 2} \right)^2} + y_0^2.\)
Vì \(A \in (E)\) nên \({{x_0^2} \over 4} + y_0^2 = 1 \Rightarrow y_0^2 = 1 – {{x_0^2} \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
Vì AB = AC nên \({\left( {{x_0} – 2} \right)^2} + y_0^2 = 4y_0^2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\)
Thay (1) vào (2) và rút gọn ta được
\(7x_0^2 – 16{x_0} + 4 = 0 \Leftrightarrow \left[ \matrix{
{x_0} = 2 \hfill \cr
{x_0} = {2 \over 7}. \hfill \cr} \right.\)
Với \({x_0} = 2\) thay vào (1) ta có \({y_0} = 0.\) Trường hợp này loại vì \(A \equiv C.\)
Với \({x_0} = {2 \over 7}\) thay vào (1) ta có \({y_0} = \pm {{4\sqrt 3 } \over 7}.\)
Vậy \(A\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right),B\left( {{2 \over 7}; – {{4\sqrt 3 } \over 7}} \right)\) hoặc \(A\left( {{2 \over 7}; – {{4\sqrt 3 } \over 7}} \right),B\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right)\)

